This is possible when y is greater than y ≥ 5 Hence, the range of f(x) is 5, ∞) Example 2 Find the domain and range of a function f(x) = (2x – 1)/(x 4) Solution Given function is f(x) = (2x – 1)/(x 4) We know that the domain of a function is the set of input values for f, in which the function is real and definedWrite the domain and range in setbuilder notation and interval notation find the inverse of f(x)=(1/2x2)sq Determine whether it is function and state its domain and range asked in ALGEBRA 2 by payton Apprentice domainofafunction
2
Y=x^2-2x-3 domain and range
Y=x^2-2x-3 domain and range- Find the domain of each of the following functions given by f(x) = (x^3 x 3)/(x^2 1) asked in Sets, Relations and Functions by RamanKumar ( 500k points) setsAlgebra Find the Domain and Range f (x)=x^22x3 f (x) = x2 − 2x − 3 f ( x) = x 2 2 x 3 The domain of the expression is all real numbers except where the expression is undefined In this case, there is no real number that makes the expression undefined Interval Notation




Inverse Of Quadratic Function Chilimath
Stack Exchange network consists of 178 Q&A communities including Stack Overflow, the largest, most trusted online community for developers to learn, share their knowledge, and build their careers Visit Stack ExchangeQuestion Given the function, f (x)= 2/x^22x3 find tthe domain and range by showing your work After that, find the x and y intercepts Answer by Fombitz () ( Show Source ) You can put this solution on YOUR website!300 seconds Q The graph of an exponential function is shown on the grid Based on the graph, which statement about the function is true?
That is, you need 1 x − y 2 ≥ 0 or "in more simple terms" 1 x ≥ y 2 So ( f ( x, y)) = { 1 x ≥ y 2 ∣ x, y ∈ R } The range is slightly more tricky but not so much Since x and y are allowed to be anything in R (so long as they are in the domain), we can work out a way for all of nonnegative R to be mapped toThe domain is where x 2 − 2 x − 8 is real, so the domain is x ≥ 4 or x ≤ 2 As for the range, if the square root function returns only the positive root, the range is y ≥ 0 To see this, note that 0 is in the range ( x = − 2 , x = 4 ) , that the function is continuous over the domain of x (so every y between the minimum and maximum is in the range), and the lim x → ∞ x 2 − 2 x − 8 = lim x → −Now y = 2x^2 2domain of x is all real numbers as abovebut as far as range is concerned we see that since square of x is always positive,its minimum value can be 0hence (square of x) has a maximum value of 0hence has a maximum value of 1 hence y has a maximum value of 2 hence range of y is all real numbers less than or equal to 2
So, its domain of f(x) is all real numbers But value of f(x) can not be less than 1 because for x = 0 the value of f(x) is 1 and also for any values of x, the value of f(x) can never be less than 1 So, Range of f(x) is all real numbers greater than 0 Hence, Domain and Range of f(x) is given by Domain {x all real numbers} ;The same applies to the vertical extent of the graph, so the domain and range include all real numbers Figure 18 For the reciprocal function f ( x) = 1 x, f ( x) = 1 x, we cannot divide by 0, so we must exclude 0 from the domain Further, 1 divided by any value can never be 0, so the range also will not include 0Which integer is not in the range?



Find The Domain And Range Of Each Of The Following Gauthmath
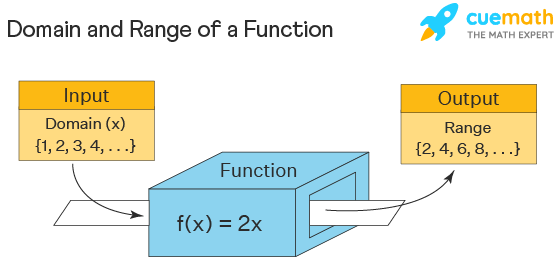



Domain And Range Examples Domain And Range Of A Function
Domain and range of z = x^2 y^2 WolframAlpha Volume of a cylinder?Question 3 Find the domain and range of y = 2 arcsin(3 x 1) Solution to question 3 1 Domain To find the domain, we need to impose the following condition 1 ≤ (3 x 1) ≤ 1 solve to obtain domain as 0 ≤ x ≤ 2 / 3 2 Range The range of arcsin(3x 1) is the same as the range of arcsin(x) which is pi / 2 ≤ y ≤ pi / 2 HenceAlgebra Find the Domain and Range y=x^23 y = x2 3 y = x 2 3 The domain of the expression is all real numbers except where the expression is undefined In this case, there is no real number that makes the expression undefined Interval Notation (−∞,∞) ( ∞, ∞) Set Builder Notation {xx ∈ R} { x x ∈ ℝ }




Domain And Range Of 1 X 2 2x 8 Youtube




Solved Find The Domain And Range Of The Functions G X Y Chegg Com
3 = 2 Thus, we can write our range in the following two ways R (1 ;2) (2;1) (10) R fyjy 6= 2 g (11) Notice The function is graphed in red and the vertical line in blue is our asymptote where our domain gap is as well Example 2 h(x) = p x 4 (12) We don't have any fractions or logs here but we do have a square root and we knowAnswer choices The range is the set of all real numbers less than 0 The domain is the set of all real numbers greater than 4 The range is the set of all real numbers greater than 0Find stepbystep Algebra 2 solutions and your answer to the following textbook question What are the domain and range of each function?



2



1
So the Domain is all Real numbers except x = 3 Range all the values that y will be after we put all the domain values ( some time it could be a bit tricky ) One way to find the Range is to Solve for x ( find the inverse ) y(x3) = 2 → yx 3y = 2 → yx = 23y → x = (23y)/y So, y can not be 0 that means the Range is all real numbers Except y = 0 Brainly User for domain x2 is not equal to zero so x is not equal to 2 domain is R {2} its range is {1,1} because it will give only 1 or 1 for any x belongs to R {2} we have function x2/lx2l we know that lx2l= (x2) according to values of x so (x2)/ (x2) =1A Relation R is given by the set {(x, y)/y = x 3, x ∈ {0, 1, 2, 3, 4, 5}} Determine its domain and range




Find Domain And Range Of Function Y 1 X 2 16 Youtube




6 Ways To Find The Domain Of A Function Wikihow
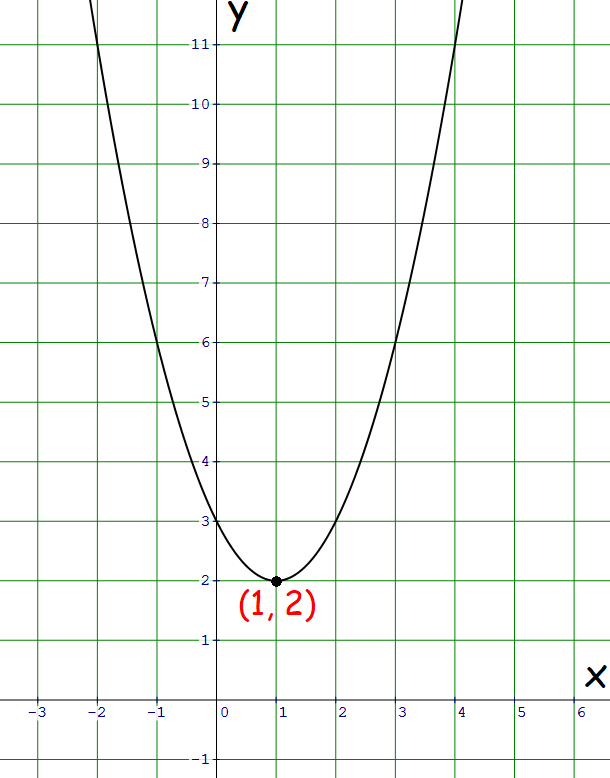
Cara Mencari Domain dan Range Fungsi Setiap fungsi memiliki dua variabel, yaitu variabel bebas dan variabel terikat Secara harfiah nilai variabel terikat "tergantung" pada variabel bebas Sebagai contoh, dalam fungsi y = f(x) = 2x y, xThe parabola has a maximum value at y = 2 and it can go down as low as it wants The range is simply y ≤ 2 The summary of domain and range is the following Example 4 Find the domain and range of the quadratic function y = {x^2} 4x 1 Just like our previous examples, a quadratic function will always have a domain of all x valuesThe function never goes below 0 So f of x so 0 is less than or equal to f of x It does equal 0 right over here f of negative 4 is 0 And then the highest y value or the highest value that f of x obtains in this function definition is 8 f of 7 is 8 It never gets above 8, but it does equal 8 right over here when x is equal to 7
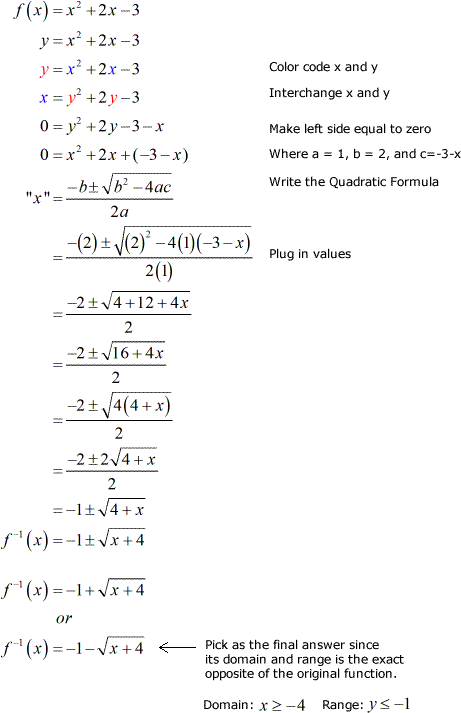



Inverse Of Quadratic Function Chilimath




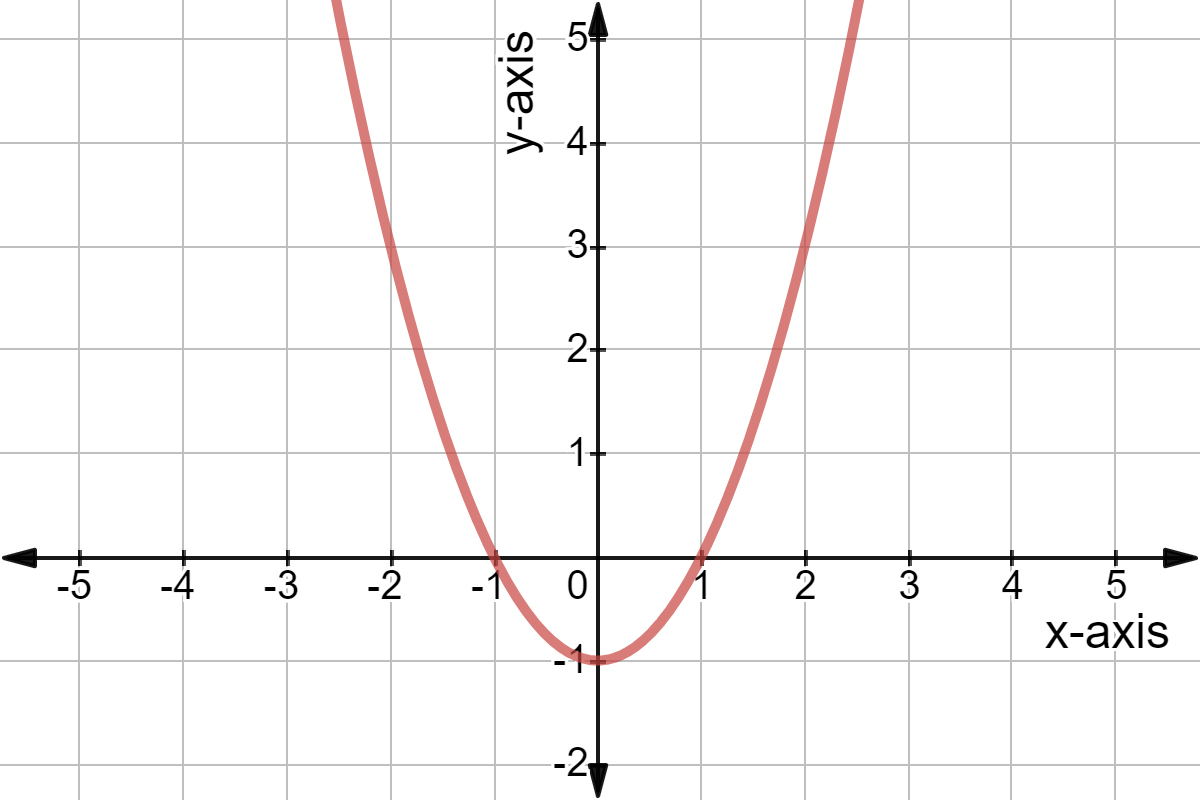
What Is The Range And The Domain Of F X X2 2x 3 Brainly Com
–1 x 2 4 y 021 Mathematics Learning Centre, University of Sydney 5 State its domain and range Solution The function is defined for all real xThe vertex of the function is at (1,1) and therfore the range of the function is all real y ≥ 1 12 Specifying or restricting the domain of a functionStep 2 Now click the button "Calculate Domain and Range" to get the output Step 3 Finally, the domain and range will be displayed in the new window What is Meant by Domain and Range? Solution The domain is the first component of the ordered pairs Whereas, Range is the Second Component of the ordered pairs Remove the duplicates if any are present Domain = {4, 1, 2, 7, 6} Range = {3, 7, 3, 5, 2}




Ex 2 2 6 Determine Domain And Range Of R X X 5




6 Ways To Find The Domain Of A Function Wikihow
In Mathematics, a domain is defined as the set of possible values "x" of a function which will give the output value "y" Answer The range of values for the function is (2,4,33,31) Stepbystep explanation Given the expression y=1/2x3 in the domain (2, 0, 2, 4) Step one for x= 2 we have y=1/(2*2)3 y=1/43 y=1/13 y=13 y=2 Step two If x is 0 we have y=1/2*03 y=1/03 y=13 y=4 step three if x is 2 y=1/2*23 y=1/43 y=13/4 y=325 y =33 StepThe first position can be filled with 1 or 2 or 3, therefore there are three different ways to fill the first one The second and the third position can be filled with three different ways, too



How To Find The




Discontinuity Calculator Wolfram Alpha
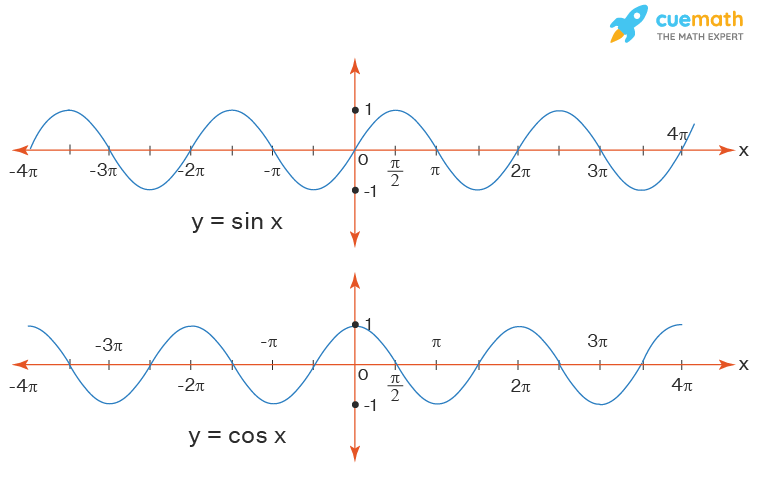
Cos x \displaystyle \cos x cosx is all the real numbers, therefore the domain of f ( x) = sin x cos x \displaystyle f (x)=\sin x\cos x f (x) = sinxcosx is all the real numbers, too Now for finding the range of f \displaystyle f f, one should know the formula which is given below The range is the values of y when x lies in the domain The tangent function is periodic with a periodicity of pi Here, y = tan (2x pi) For the set of Find the domain, range, asymptote, the x and y intercepts then graph y= f(x)= 3^(x2) 1 Educator answer eNotescom will help you with any book or any question
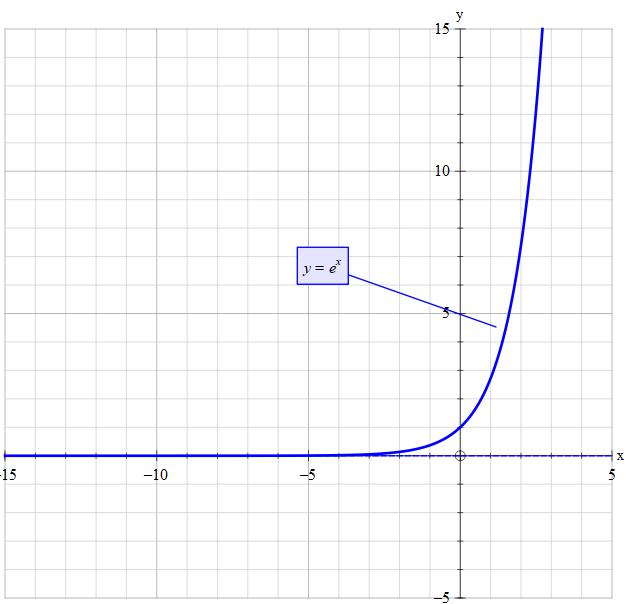



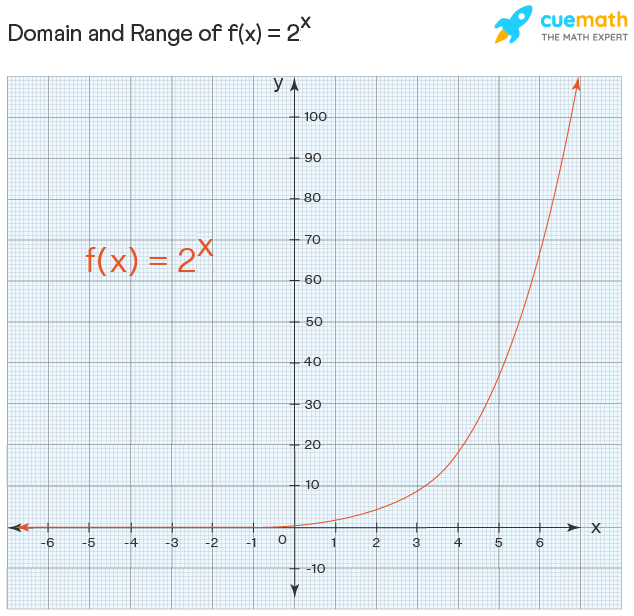
What Is The Domain And Range Of Y E X Socratic




L1 Functions Domain Amp Range
Domain and range graph The graph of f(x)=x2 f ( x) = x 2 (red) has the same domain (input values) as the graph of f(x)=− 1 12x3 f ( x) = − 1 12 x 3 (blue) since all real numbers can be input values However, the range of the red graph is restricted to only f(x)≥0 f ( x) ≥ 0, or y y values above or equal to 0 0 To find The domain and range of the real function Solution To find domain Equate the denominator to zero Denominator (3x)=0 x=3 This means at x=3 function is not defined And by definition of domain The domain is where the function is not defined Domain is Range Put f(x)=y Range is the set of value that correspond to domain#Domain #Range #FunctionsFind the Domain and the Range of the square root function y = square root of (1 x^2)Learn more about functions here https//wwwf




For A Quadratic Function Find Vertex Axis Of Symmetry Domain And Range Intercepts Youtube




Range And Domain Of Y X 2 18x 5 And Y 2x 2 12x 3 Brainly Ph
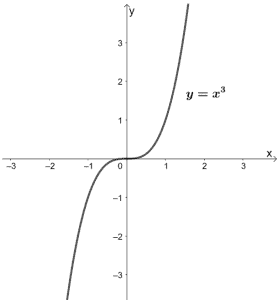
The function is y = x 3 2 Domain of the function is the set of all real numbers Since, x 3 is either positive or zero for x = 3, the range of the function is given by the interval 0, infinity answered by lilly Expert The function is y = x 3 2Piece of cake Unlock StepbyStep Natural Language Math Input NEW Use textbook math notation to enter your mathDomain\f (x)=x^3 domain\f (x)=\ln (x5) domain\f (x)=\frac {1} {x^2} domain\y=\frac {x} {x^26x8} domain\f (x)=\sqrt {x3} domain\f (x)=\cos (2x5) domain\f (x)=\sin (3x) precalculusfunctiondomaincalculator en




Misc 3 Find Domain Of F X X2 2x 1 X2 8x 12



Find The Domain And Range Of Xy X 3y 1 Mathskey Com
Explanation y = √x2 −3x 2 = √(x −1)(x − 2);Even though they are represented differently, the above are the same function, and the domain of the function is x = {2, 3, 5, 6, 8} and the range is y = {4, 8, 2, 9, 3}This is how you can defined the domain and range for discrete functionsDomain y= (x^2x1)/x full pad » x^2 x^ {\msquare} \log_ {\msquare} \sqrt {\square} \nthroot \msquare {\square} \le \ge



Find Domain And Range Of Function Y 1 X 2 16 Youtube



1
#Domain #Range #Functions #Algebra #MathematicsFind the domain and the range of the function y = 2 (x^2)/(x^2 4)Learn more about functions here https//Domain under root should be ≥ 0 ∴ (x −1)(x − 2) ≥ 0 When 1 < x < 2 sign of y is ( )( −) = ( −) ∴ < 0 Therefore for 1 < x < 2;y is undefined Domain x ≤ 1 and x ≥ 2 or x ∣ ( − ∞,1 ∪ 2,∞) Range y ≥ 0 or y ∣ 0,∞) since square root of positive quantity is also positiveDomain, Codomain and Range of a Relation The domain of the relation R ={x ∈ A x R y, for some y ∈ B} The codomain of the relation R is B The range of the relation R ={y ∈ B x R y, for some x ∈ A} From these definitions, we note that domain of R ⊆ A, codomain of R = B and range of R ⊆ B Solved Questions



What Is The Range Of A Function Expii



If F X X 2 2x 3 What Is The Range With Steps Quora
Range {y y > 0}1) −4 2) −2 3) 0 4) 7 3 If the domain of f(x) =2x3 is {−3There are only two restrictions on x that make the denominator go to zero So and are excluded from the domain



Find The Domain And Range Y X 2 2x 3 Displaystyle Y X 2 2x 3 Snapsolve
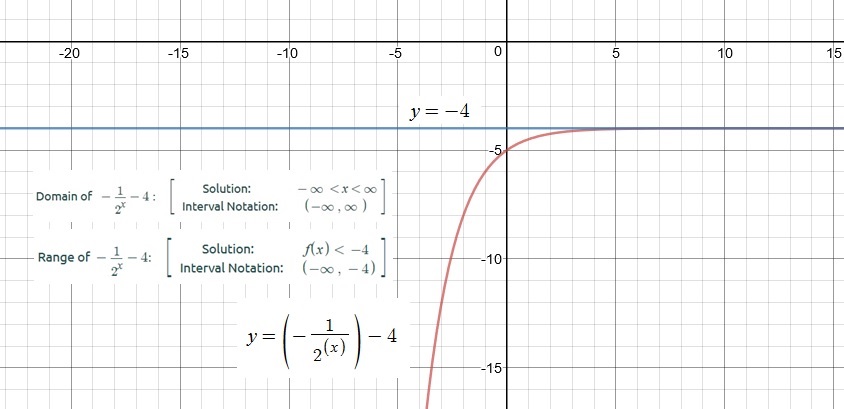



What Is The Domain And Range Of Y 2 X 4 Socratic




How To Find Domain And Range From A Graph Video Khan Academy




How To Find The Domain Of A Function Video Khan Academy



Parent Functions Types Properties Examples




Solved 3 Find The Domain And Range Of The Function H X Y Chegg Com



Functions Domain And Range Purplemath



Domain Range Functions Slope Bingo Card




Write Domain And Range Given An Equation College Algebra




Find The Domain And Range Of X2 2x 4 X2 2x 4 Where X Belongs To Real Maths Relations And Functions Meritnation Com
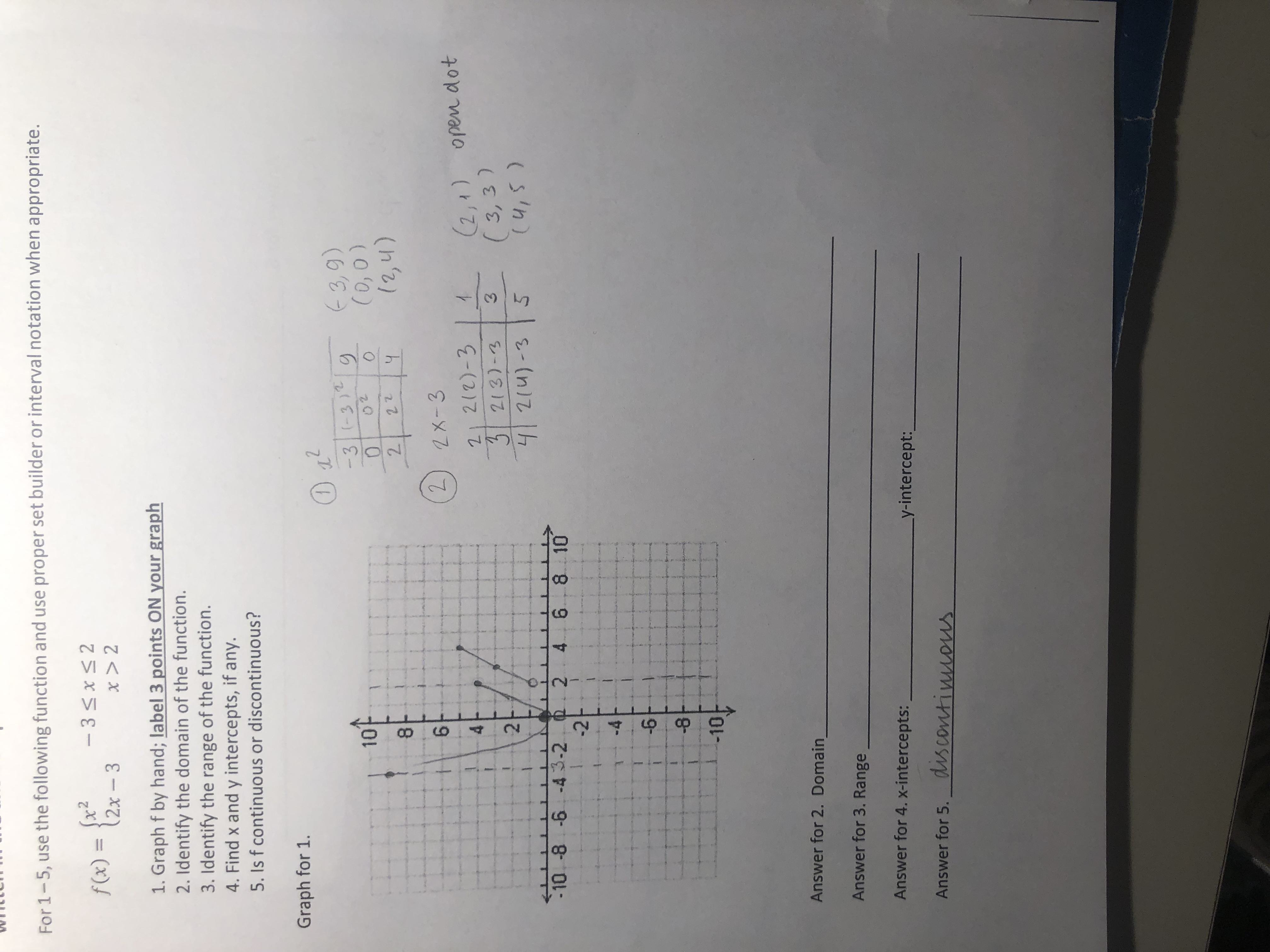



Answered For 1 5 Use The Following Function And Bartleby




Domain And Range Of 2x 3 X 2 A Rational Function Youtube
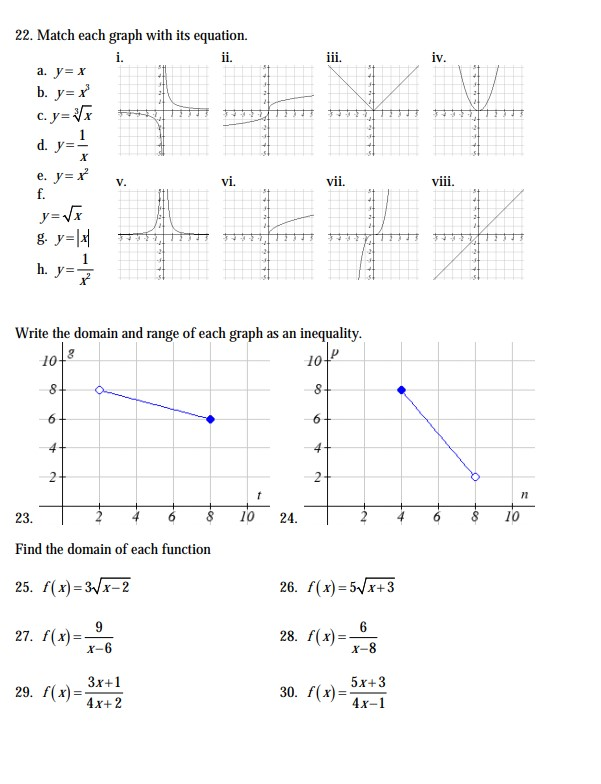



Find The Domain And Range Of The Function F X X 2 9 X 3 Donimain



How To Find The Domain And Range From Y X 2 2x 8 Quora



Domain And Range Of Rational Functions




Inverse Of Quadratic Function Chilimath



Solution What Is The Domain And Range Of 3y X 2 X 1 4 2x 3
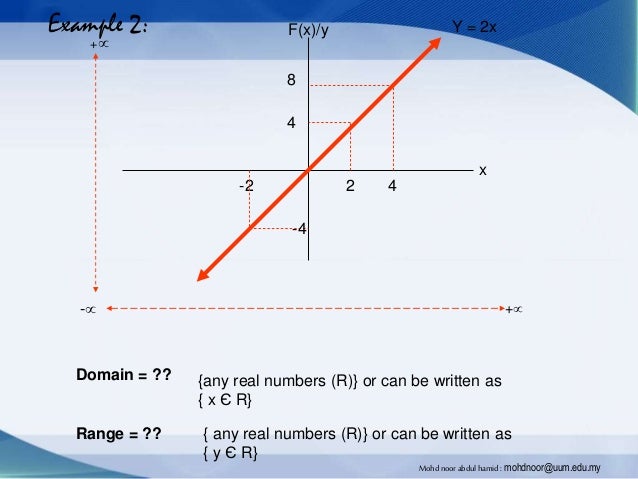



Introduction To Function Domain And Range Mohd Noor



Solved Find The Domain And Range For The Function F X 2x 2 5 Course Hero




Finding Domain And Range




Domain And Range Of Functions
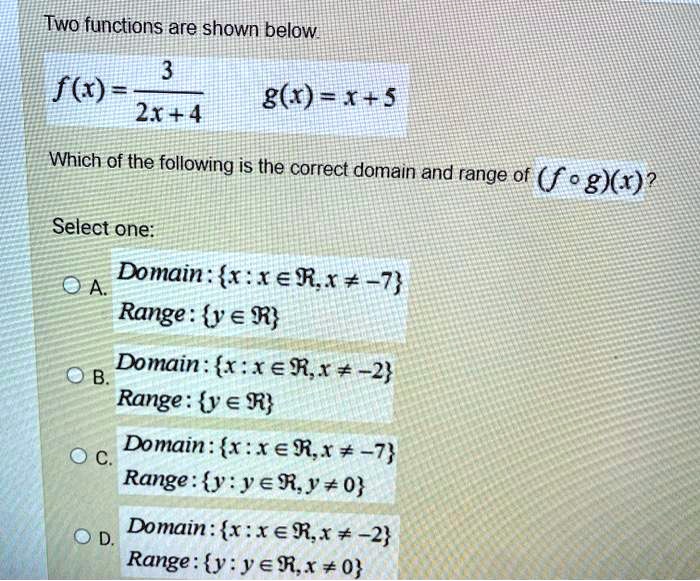



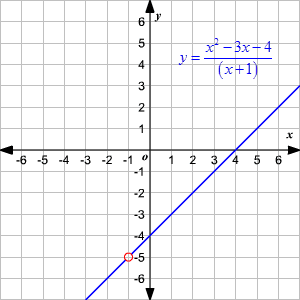
Solved Two Functions Are Shown Below 3 F G R 5 2x 4 Which Of The Following Is The Correct Domain And Range Of F O G X Select One A Domain Xerx 7 Range



1
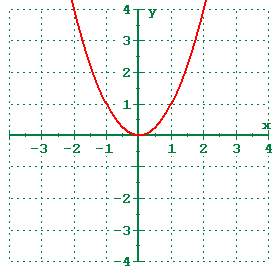



1 5 Shifting Reflecting And Stretching Graphs
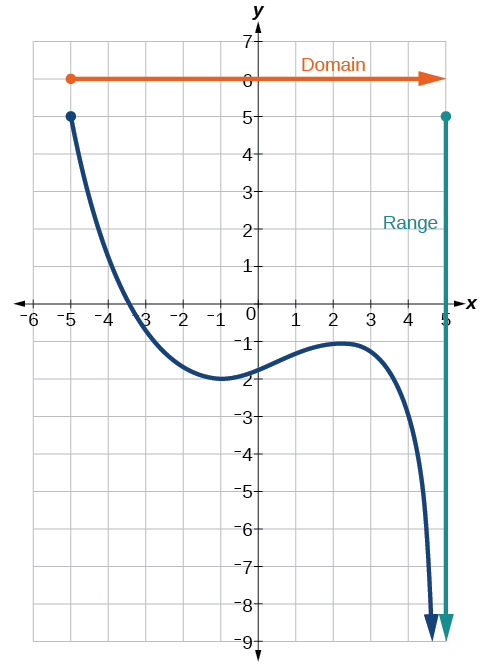



3 3 Domain And Range Mathematics Libretexts




Solved Find The Domain Range The X And Y Intercepts And Sketch The Graph B Y Kx 4 C Y K 1 2 A Y Vx 2 D Y Vx 2 7 Find The Domain In Interval Notation For The Following




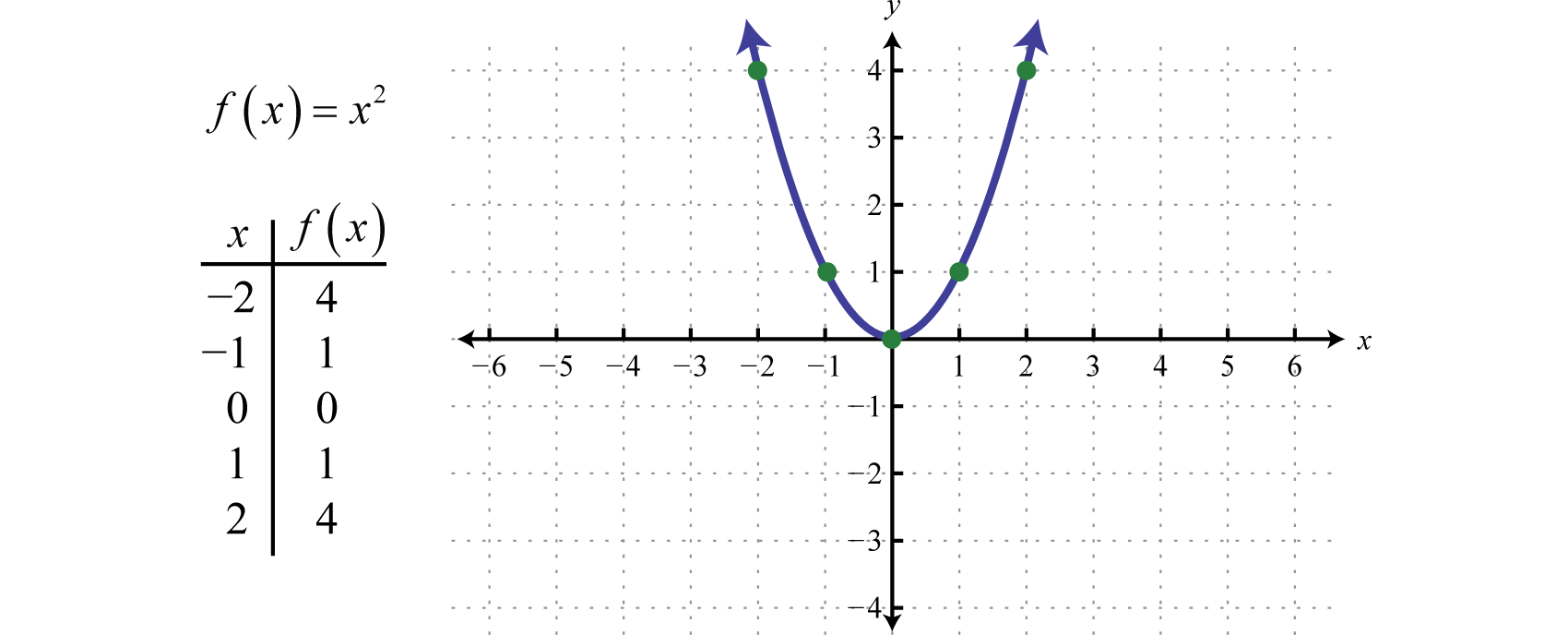
Answered Function Domain X Range Y Y X2 Bartleby




Chapter 1 Practice Exercises




Solved In Problems 1 8 Find The Domain And Range Of The Chegg Com




Identify The Range Of Y X 2x 3 If The Domain Is All Real Numbers Brainly Com




Question 8 4 Points Listen Find The Domain And The Ra Math




Solved Find The Domain And Range Of Each Function 1 Y X 7 2 Y Vx 10 3 Y X2 25 4 Y 5x2 2x 3 5 Y X Z



What Is The Y Intercept X Intercept Range Horizontal Asymptote Vertical Asymptote And Domain Of This Inverse F X X 1 2x 6 Quora
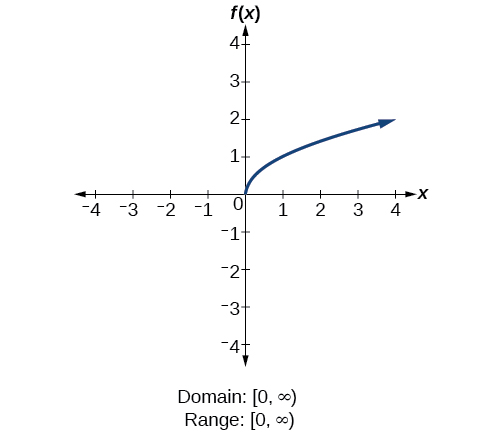



Domain And Range Algebra And Trigonometry
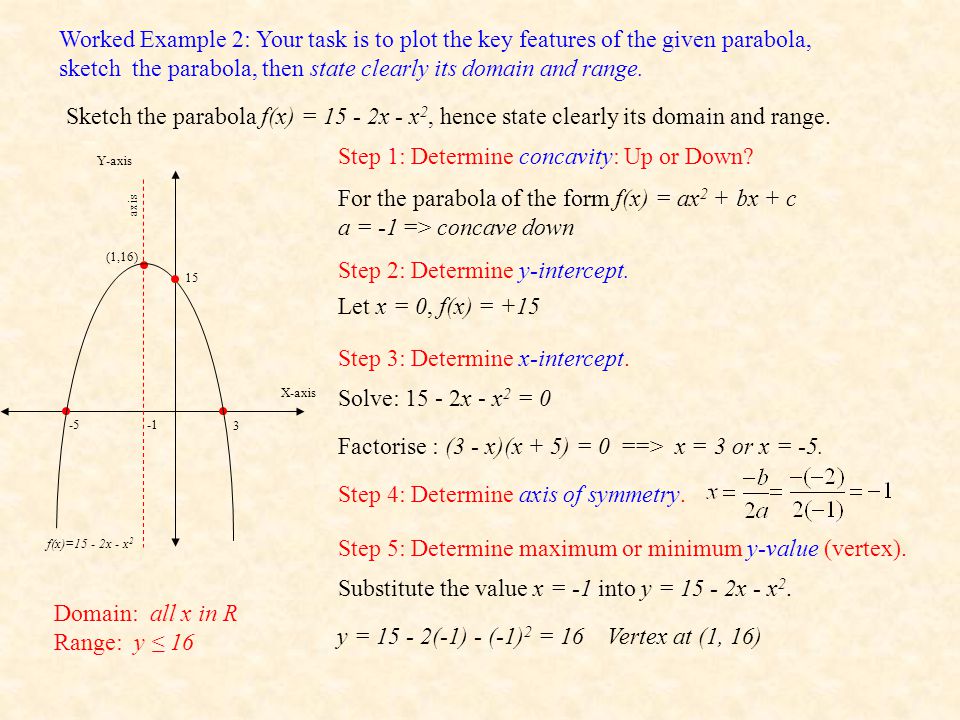



Functions Domain And Range By Mr Porter Ppt Download
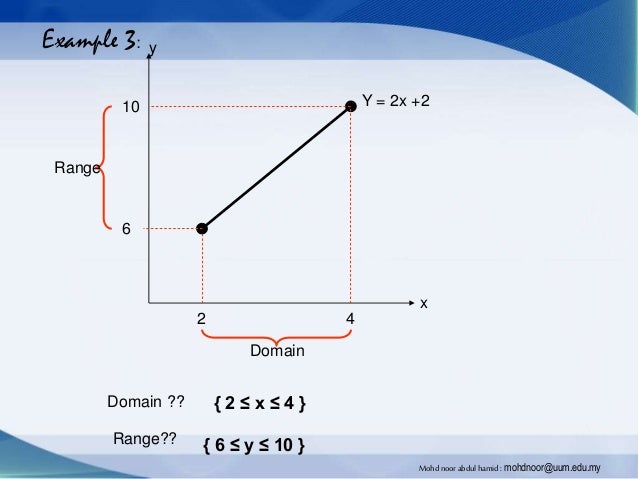



Introduction To Function Domain And Range Mohd Noor




Find The Domain And Range Of F X Xx 2 2x 3




Finding Domain And Range



Domain And Range Examples Domain And Range Of A Function
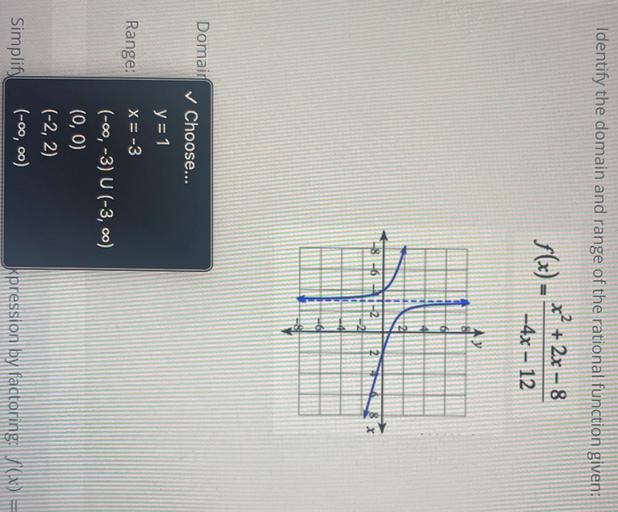



Identify The Domain And Range Of The Rational Function Math



2




Exercise 1 3 Functions Problem Questions With Answer Solution




Find The X And Y Intercepts Domain And Range And Sketch A Graph



Quadratic Functions And Their Graphs




The Domain Of The Function Cos 1 2x 1 Is



How To Find Domain And Range Video Practice Questions




Solved 2 Find The Vertex Domain Range X And Y Chegg Com



Lesson 2 Graphing Inverse Functions Notes Mathematics Itt3014 Studocu



Domain And Range Examples Domain And Range Of A Function



How Do You Find The Domain And Range Of Y 3x 2 Socratic



Solution Given The Function F X 2 X 2 2x 3 Find Tthe Domain And Range By Showing Your Work After That Find The X And Y Intercepts



Domain And Range Of A Function




Graph The Quadratic Function Y X 2 2x 3 Vertex X Y Intercepts Symmetry Domain Range Youtube




Ppt Function Iii Powerpoint Presentation Free Download Id
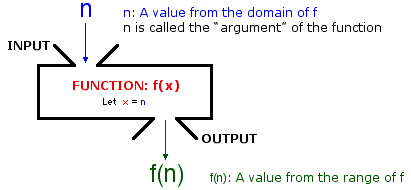



Function



How To Get The Domain And Range Of The Rational Function G X X 3 X 1 2x 2 5x 3 Quora
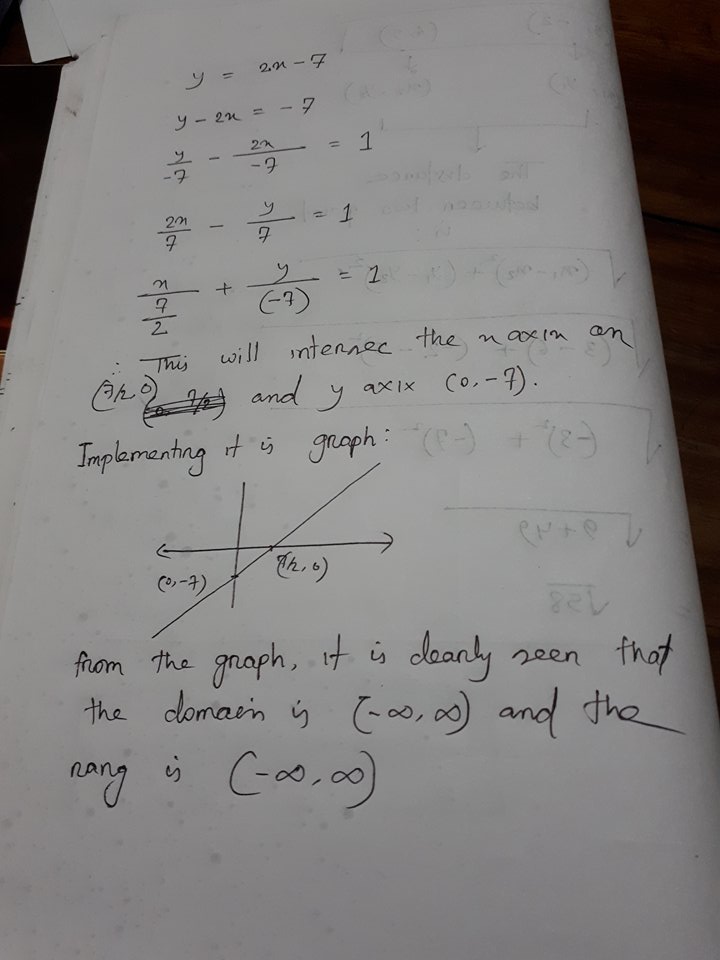



What Is The Domain And Range Of Y 2x 7 Socratic




How To Find The Domain And Range Of A Function 14 Steps
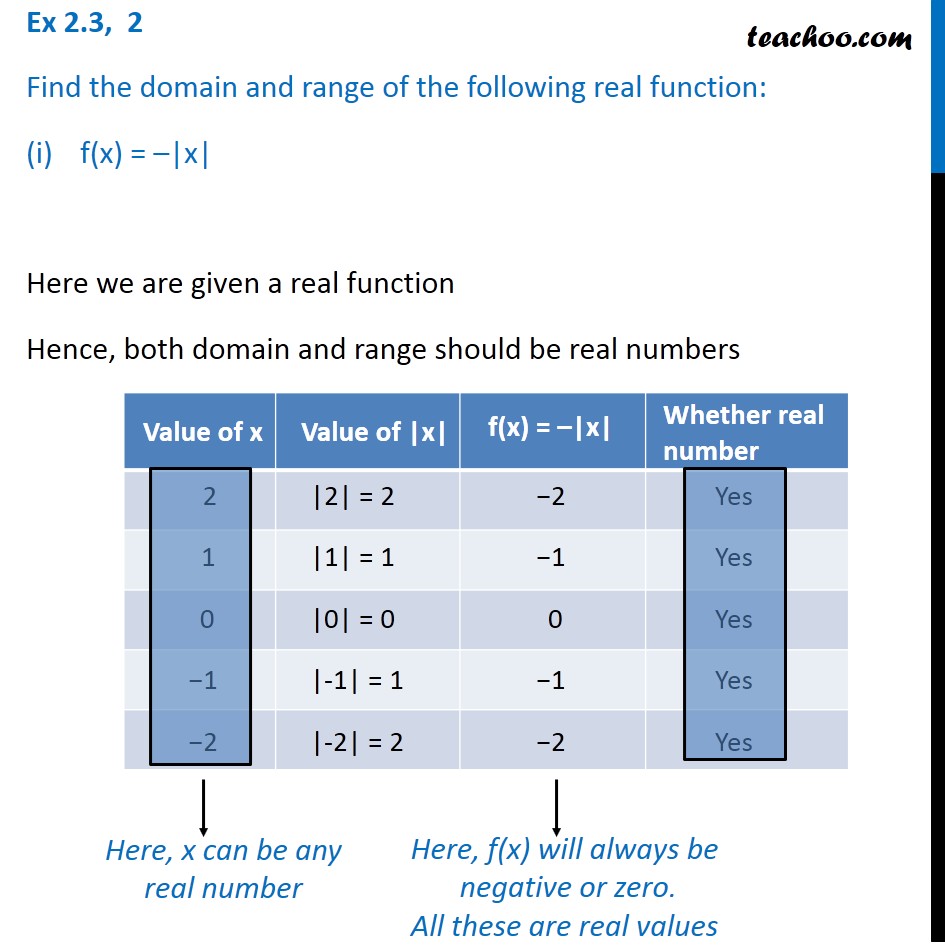



Ex 2 3 2 Find The Domain And Range Of The Function F X X




Domain Range Of A Straight Line Y 2x 3 For Polar Coordinate 8 Mathematics Stack Exchange



What Is The Domain Intercepts Range And Asymptote Of 2x X 2x 3 Quora
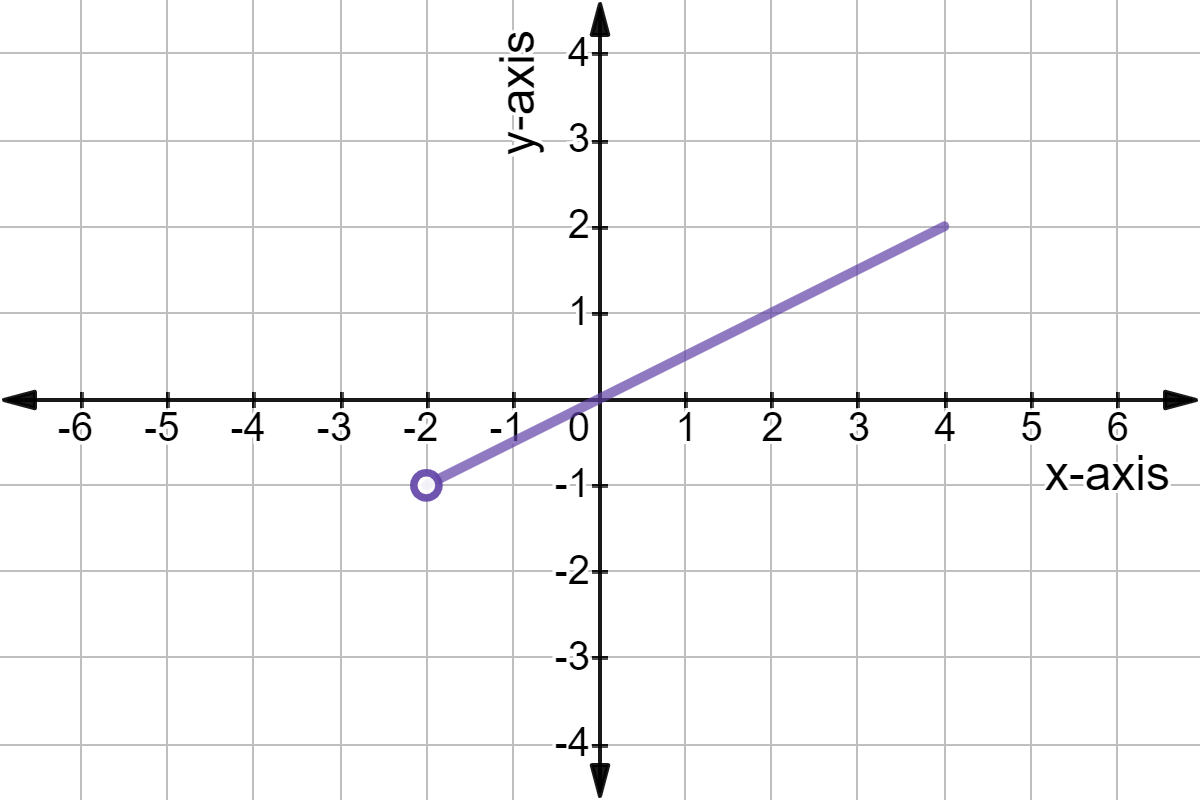



What Is The Range Of A Function Expii




A Find The Domain And Range And Write In Interval Notation B What Are The X And Y Intercepts As Ordered Pairs Study Com



Find The Domain And Range Of F X 2x 5 Mathskey Com



Find The Domain And Range Of The Following Rationa Gauthmath



What Is The Domain Intercepts Range And Asymptote Of 2x X 2x 3 Quora




Functions Domain And Range By Mr Porter Ppt Download
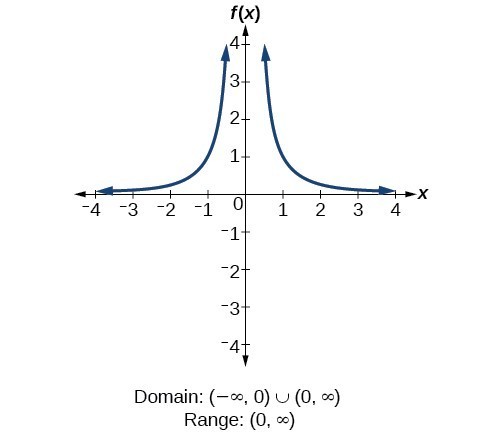



Determine Domain And Range From A Graph College Algebra




How To Find The Domain And Range Of A Function 14 Steps



2
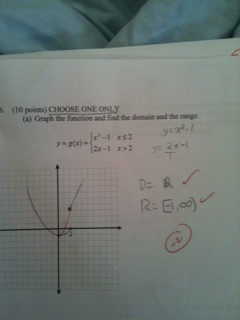



Solved Graph The Function And Find The Domain And Range Chegg Com
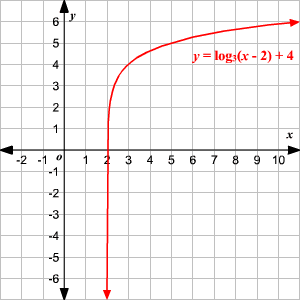



Domain And Range Of Exponential And Logarithmic Functions



Y X 3 3x 2 4 Y X 3 3x 2 45x 1 Yenhoroblogsip
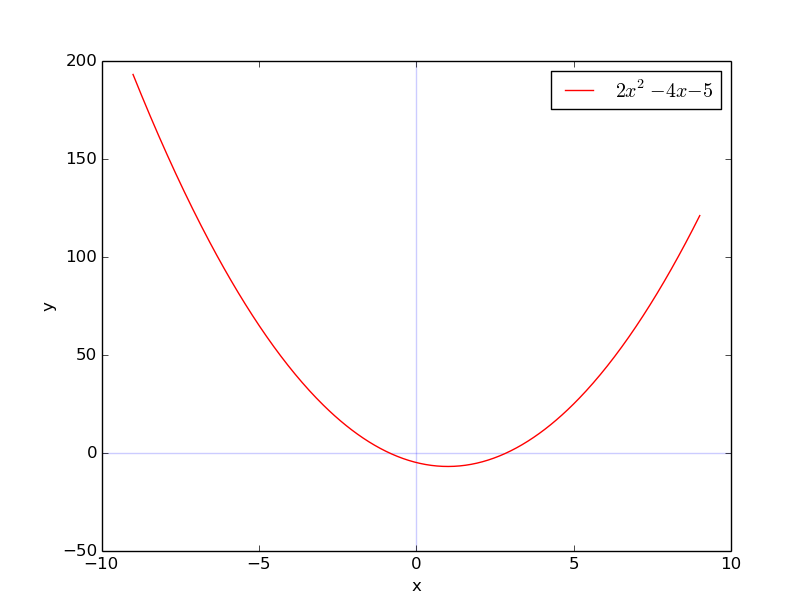



How Do You Find The Domain And Range Of Y 2x 2 4x 5 Socratic
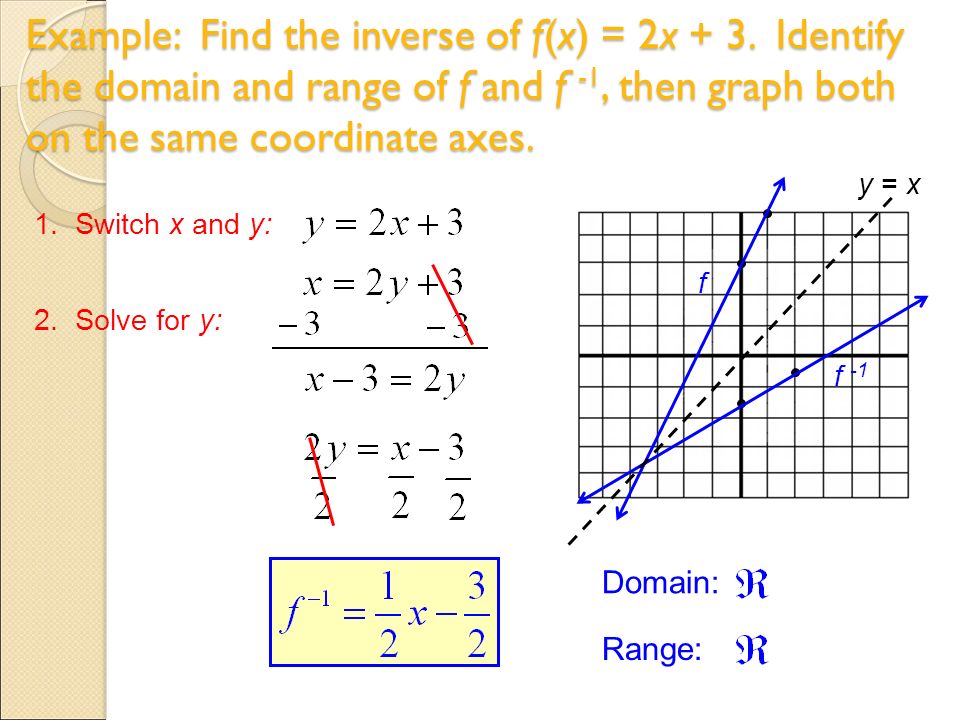



More Quarter Test Review Section 4 1 Composite Functions Ppt Download



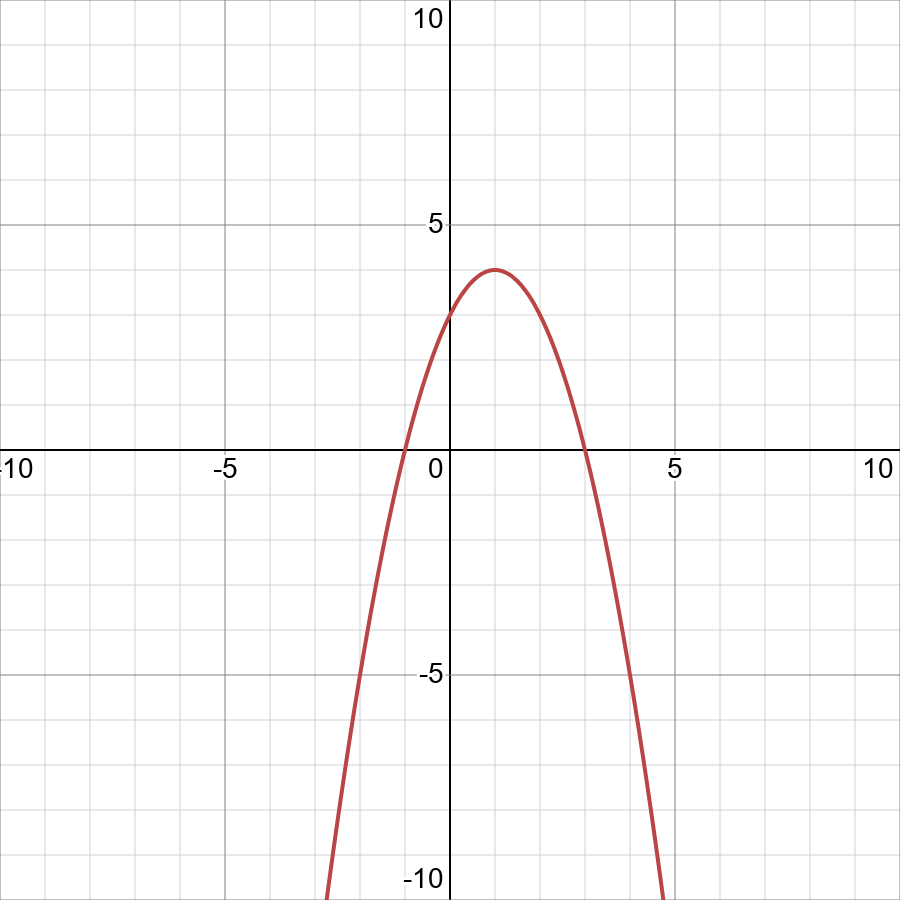
Solution Y 2x 2 X 6 Find The Vertex Min Or Max Zero 39 S Y Intercept Axis Of Symmetry Wider Or Thinner Domain Range




Solved Evaluate The Following Find The Domain And Range Chegg Com
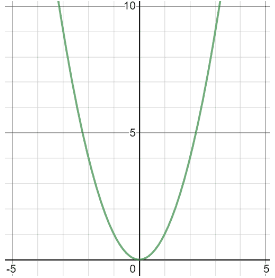



Domain And Range



Find The Domain And Range Y 2x 3 4x 7 Y X 2 X 2 Gauthmath




Example 10 R X Y Y 2x What Is Domain Codomain Range


