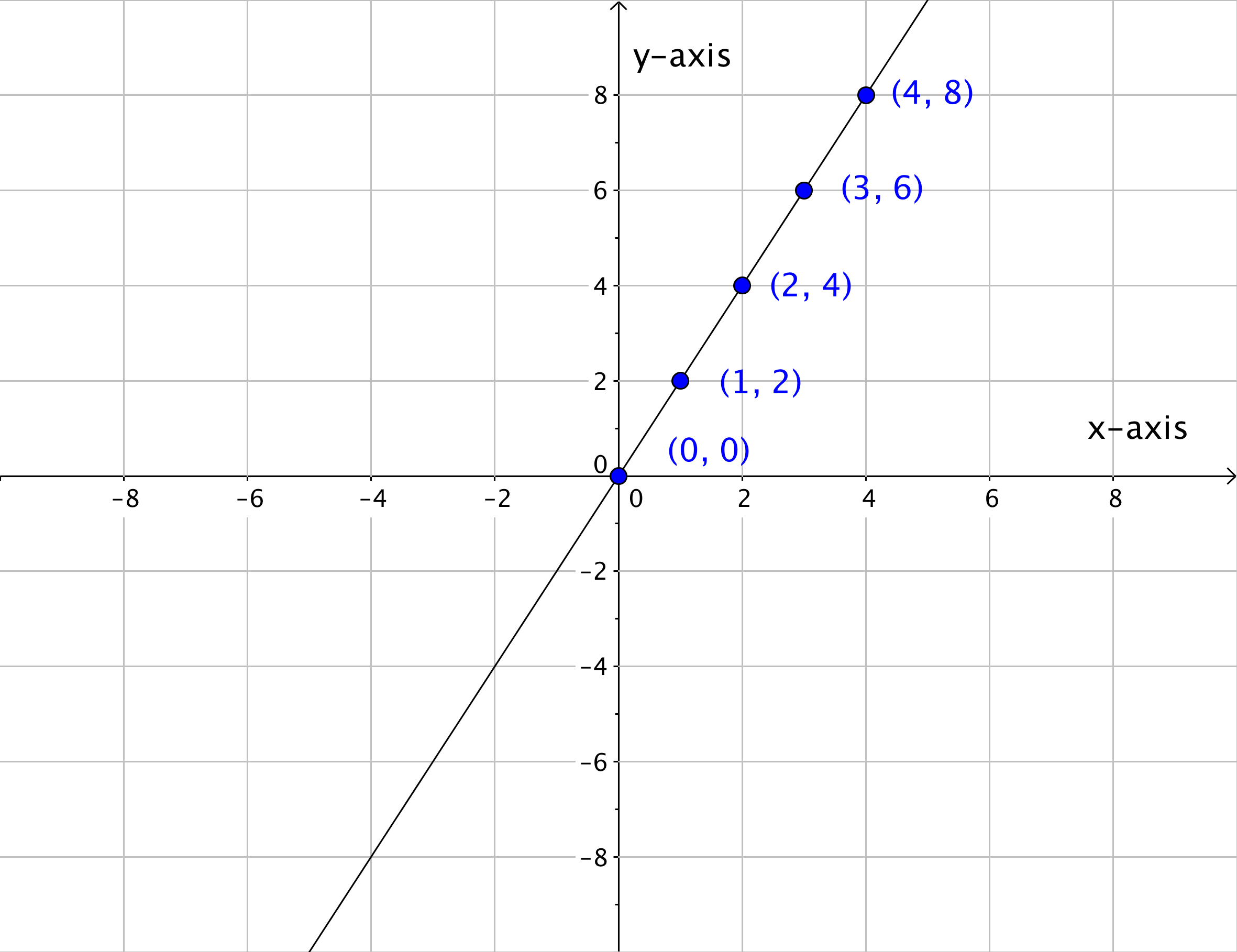
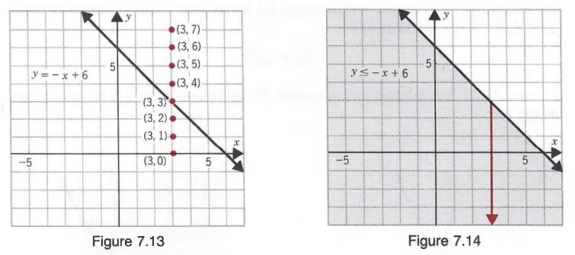
Form the table, it is observed that, the rate of change between x and y is 3 This can be written using the linear function y= x3 Linear Function Formula The expression for the linear function is the formula to graph a straight line The expression for the linear equation is;A linear equation is represented as a line graph In order to draw the line graph we require several pairs of coordinates These coordinates represent the relationship given in the equationX – 4y 4 y x 1 On a coordinate plane, 2 straight lines are shown The first solid line has a positive slope and goes through (0, negative 1) and (4, 0) Everything above the line is shaded
Graphing Linear Functions Geogebra
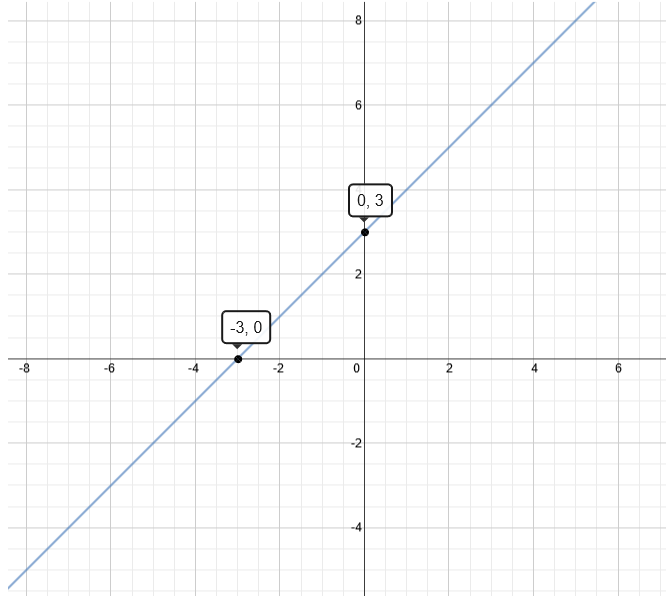
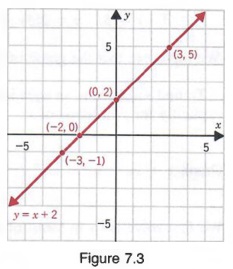
Linear graph y=x+3
Linear graph y=x+3-Advertisement For this example, it's simplest to first solve for "y =" This is especially true if I'm using a graphing calculator to fill in my Tchart, because graphing calculators can only handle line equations when they're in the form "y =" So, to make my like easier, I'll solve thisWhen x is 0, y is already 1 So 1 is also needed;
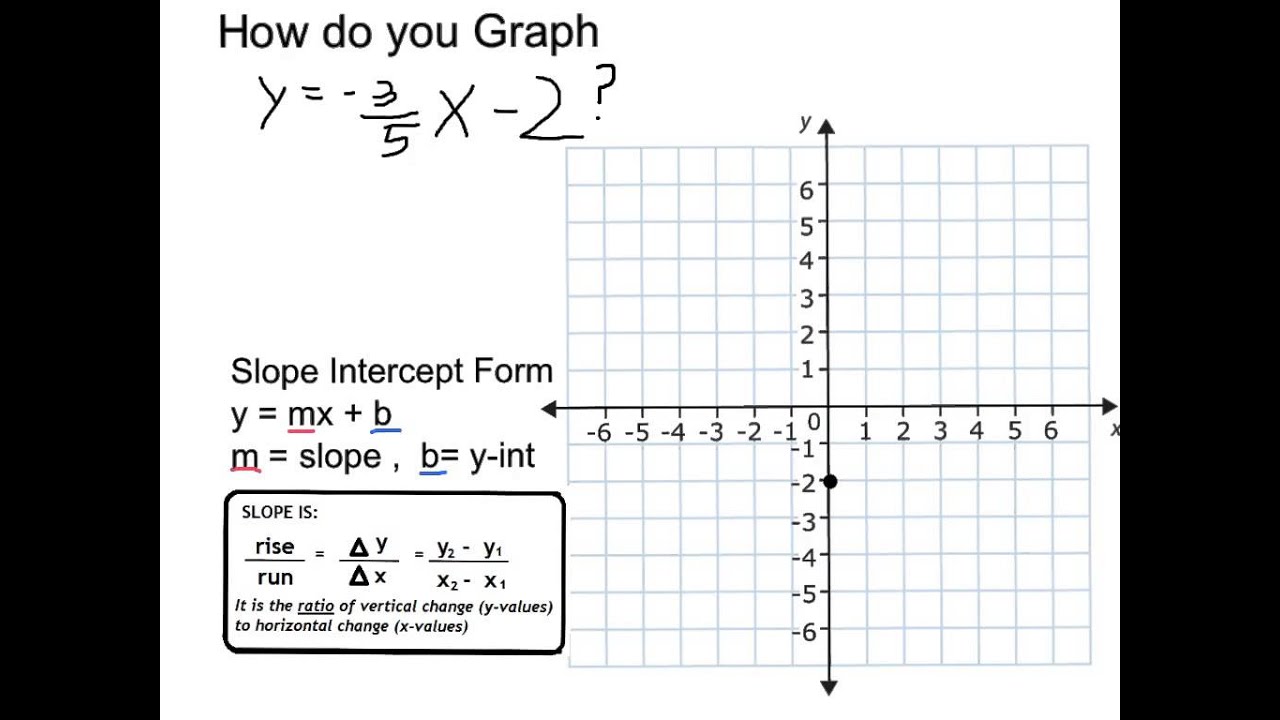



Graph Y 3 5 X 2 Youtube
Method 1 using two points to graph a linear equation The graph of any linear equation like y = 3 x 2 or y = − x 9 is a line, and only two points are needed to define a line The idea with this method is to find two points on the line by picking values of xAnd so y = 2x 1;Use the intercept method to graph xy=3 Step 1 Intercepts occur when one of the coordinates is equal to 0 So the yintercept occurs at x=0 and the xintercept occurs at y=0 Step 2 It takes two points to make a line So use these intercepts points Step 3 When x=0, then 0y=3 or y=3 So we have point (0,3) Step 4 When y=0, then x0=3 or
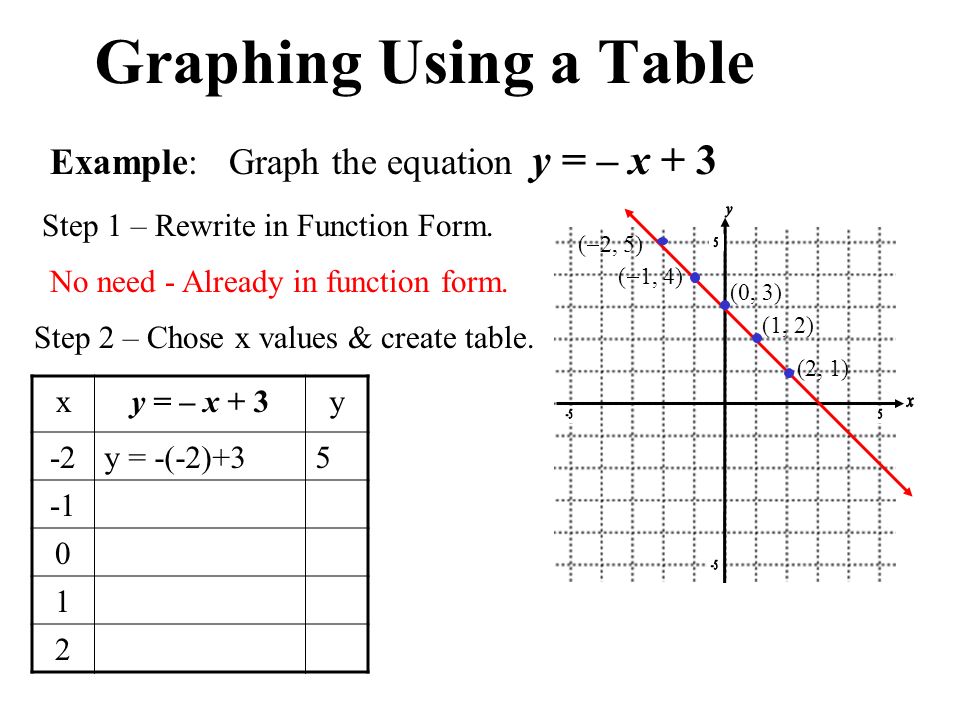
In example 3 look at the tables of values and note that for a given value of x, the value of y in the equation y = 3x 2 is two more than the corresponding value of y in the equation y = 3x Look now at the graphs of the two equations and note that the graph of y = 3x 2 seems to have the same slope as yThen click on the graph until the correct one is displayed 3 x y 1 = 0 / < It goes from the bottom left corner up into the top right corner Using graph paper, graph the following equation Then click on the graph until the correct one is displayed y = 3/5 x 12 (a) Complete the table of values for y = 1 – 2x (Total for question 2 is 5 marks) (b) On the grid draw the graph of y = 1 – 2 x for values of x from –2 to 3
Here are some example valuesY = mx c where m is the slope, c is the intercept and (x,y) areSolution for Graph each linear equation 3 x3y= 6 Q A merchant sold his entire stock of shirts and ties for $1000, the shirts being priced at 3 for $10 A Let the number of shirt sold x units Let the number of ties sold y unit
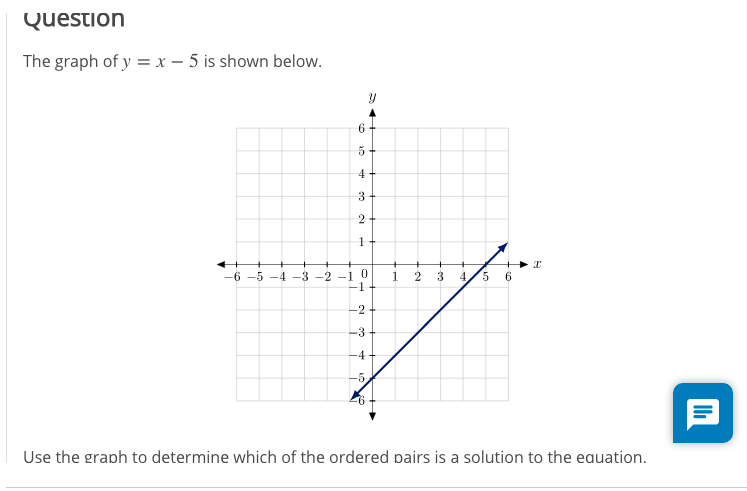



Question The Graph Of Y X 5 Is Shown Below Y 6 4 Chegg Com




A System Of Linear Equations See How To Solve It At Qanda
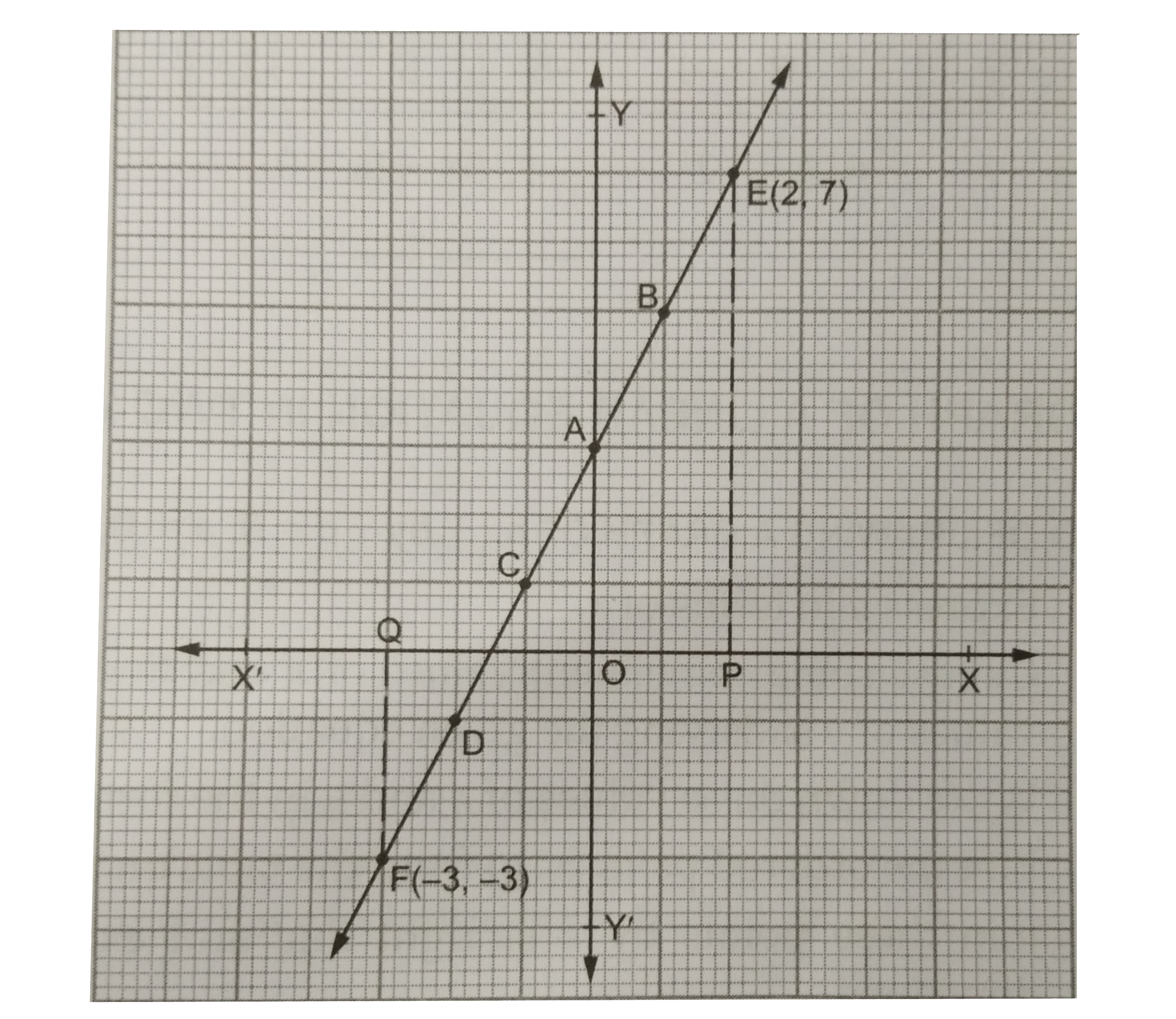
2 Find the value of p that makes the linear graph y = p − 3x pass through the point where the lines 4x − y =6 and 2x − 5y = 12 intersect 3 Faced with the problem of multiplying 5 6 times 5 3, Brook is having trouble deciding which of these four answers is correct 5 18,5 9,25 18,or 25 9 Your help is needed Once you have answered Brook's question, experiment with other examples ofFree graphing calculator instantly graphs your math problemsWe designate (3, 5) as (x 2, y 2) and (4, 2) as (x 1, y 1) Substituting into Equation (1) yields Note that we get the same result if we subsitute 4 and 2 for x 2 and y 2 and 3 and 5 for x 1 and y 1 Lines with various slopes are shown in Figure 78 below



Graph The Linear Equation Yx 2 1 Draw



Quadratics Graphing Parabolas Sparknotes
Steps for Solving Linear Equation y = 5x3 y = − 5 x 3 Swap sides so that all variable terms are on the left hand side Swap sides so that all variable terms are on the left hand side 5x3=y − 5 x 3 = y Subtract 3 from both sides Subtract 3 from both sides− q a) The x intercept is obtained by letting y = 0Linear equations A linear equation is an equation that represents a straight line When plotted on a graph, a linear equation always results in a straight line, as in the figure below, which is a special case of a linear equation referred to as the identity function, y = x



Graphing Systems Of Linear Inequalities



Quadratics Graphing Parabolas Sparknotes
Question graph the line y=x3 Answer by jim_thompson5910 () ( Show Source ) You can put this solution on YOUR website!As long as you do your work neatly and orderly, you shouldn't have much trouble with graphing linear equations Here are some more examples Graph First I'll do my Tchart Since I am multiplying the variable x by a fraction that has 3 as its denominator, I will pick xvalues that are multiples of 3 This wayClick here👆to get an answer to your question ️ Draw the graph for the linear equation given below 2x 3y = 4 Join / Login > 9th > Maths > Linear Equations in Two Variable > Graph of a Linear Equation in Two Variables Draw the graph for the each linear equation given below y = 2 3 x
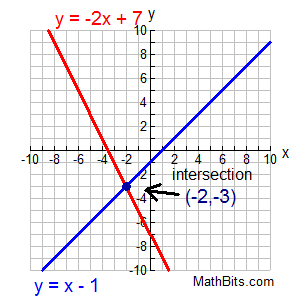



Systems Of Linear Equations Graphical Solution Mathbitsnotebook A1 Ccss Math
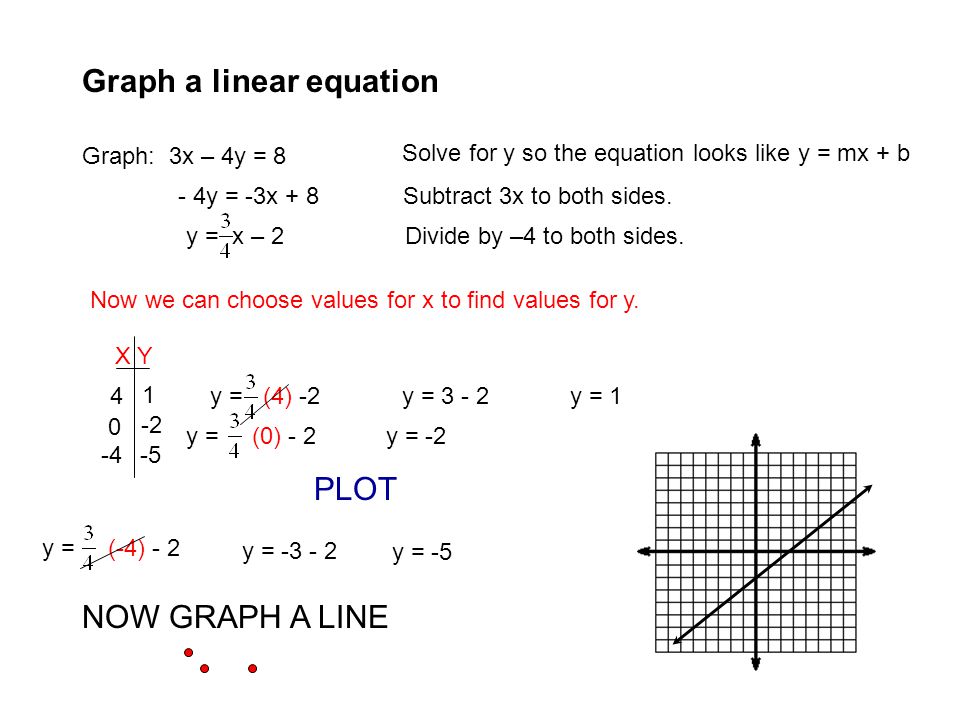



Graph A Linear Equation Graph 2x 3y 12 Solve For Y So The Equation Looks Like Y Mx B 3y 2x 12 Subtract 2x To Both Sides Y X 4 Divide Ppt Download
For example, Use your graph to solve the equation x 2 x – 2 = 0 We have already drawn the graph for y = x 2 x – 2 The other side of our equation is zero, so we need to think about the line y = 0 This is the xaxis, so look for the points where the graph crosses the xaxis The solutions are x = 1 and x = 2 To solve the equation x 2 x – 2 = 3, we would draw the line y = 3 The graph of y = x − 3 is almost the same as y = x The difference is that every point on y = x has been lowered by 3 Thus, instead of the yintercept being at y = 0 it is at y = − 3 instead Consider the generic equation of y = mx c where m is the gradient (slope) If you compare this to both y = x and y = x − 3 you will observe that there is no value shown for m (1 point) x = 2, 0, 2, 4 y = 4, 0, 4, 8 The values do not show a linear function Yes, they show a linear Math The graph represents function 1 and the equation represents function 2 A graph with numbers 0 to 4 on the xaxis and yaxis at increments of 1 A horizontal straight line is drawn joining the ordered pairs 0, 3 and 4, 3
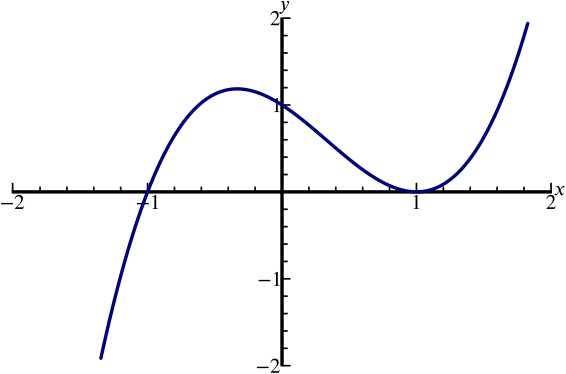



Can We Sketch The Graph Y X 3 X 2 X 1 Polynomials Rational Functions Underground Mathematics
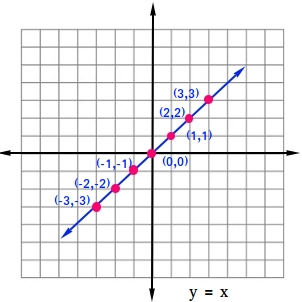



Linear Parent Function
Y = 8 – 2x y = 4 x 2 Plot the graph of the linear equations below by first forming a table of values of y using x = 0,1,2,3,4 a y = 1 2x b y = 2 x c y = 10 −x d y = 9 −2x 3 For each of these linear equations, use a graphics calculator to do the following i Plot a graph for the window given ii Generate a table of values a y = 4 x A linear inequality is an inequality that can be written in one of the following forms A x B y > C A x B y ≥ C A x B y < C A x B y ≤ C Where A and B are not both zero Recall that an inequality with one variable had many solutions For example, the solution to the inequality x>3x>3 is any number greater than 3Example y = 2x 1 is a linear equation The graph of y = 2x1 is a straight line When x increases, y increases twice as fast, so we need 2x;



Quadratics Graphing Parabolas Sparknotes



How Do You Solve Each Linear System By Graphing Y X 3 Y 2x 6 Mathskey Com
3x 2y = 1 Plot families of exponential and reciprocal graphs For example y = 2 x, y = 3 x, y = 4 x y = 1÷x, y = 2÷x, y = 3÷x, Reduce a given linear equation in two variables to the standard form y = mx c;Looking at we can see that the equation is in slopeintercept form where the slope is and the yintercept is Since this tells us that the yintercept is Remember the yintercept is the point where the graphIntercepts The general form of an invertible, linear function is y = ax q (a ≠ 0) and its inverse is y = 1 ax − q a The y intercept is obtained by letting x = 0 y = 1 a(0) − q a y = − q a This gives the point (0;




Graph The Linear Equation Yx 2 1 Draw
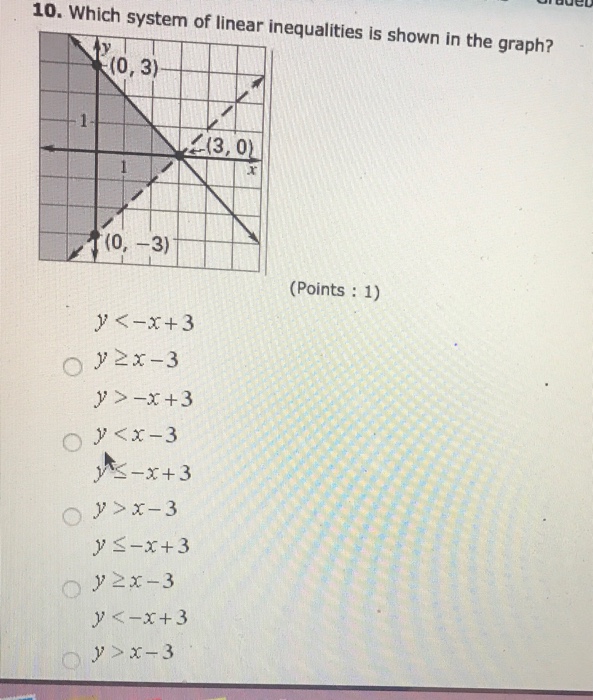



Which System Of Linear Inequalities Is Shown In The Chegg Com
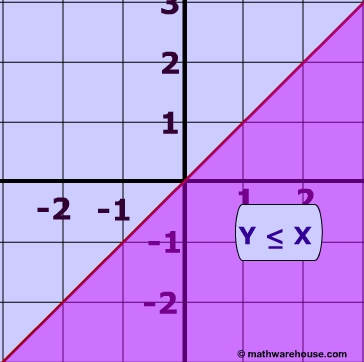
Graphing the line y = x 3 on a Cartesian Graphgraph the function y=x3 Graphing the line y = x 3 on a Cartesian Graphgraph the function y=x31 Graph the solution to y < 2x 3 2 Graph the inequality 4(x y) – 5(2x y) < 6 and answer the questions below a Check whether the point (22, 10) is within the solution set b Determine the slope of the border line 3 Graph the inequality of y< 3x and determine which quadrant will be completely shaded 4Example 3 Graph the inequality y ≤ x Compare this to the graph of y ≥ x Example 3 Solution We have two inequalities to graph here, but they use the same line We need to start by graphing y=x, which is the line that passes through the origin with a slope of 1



1
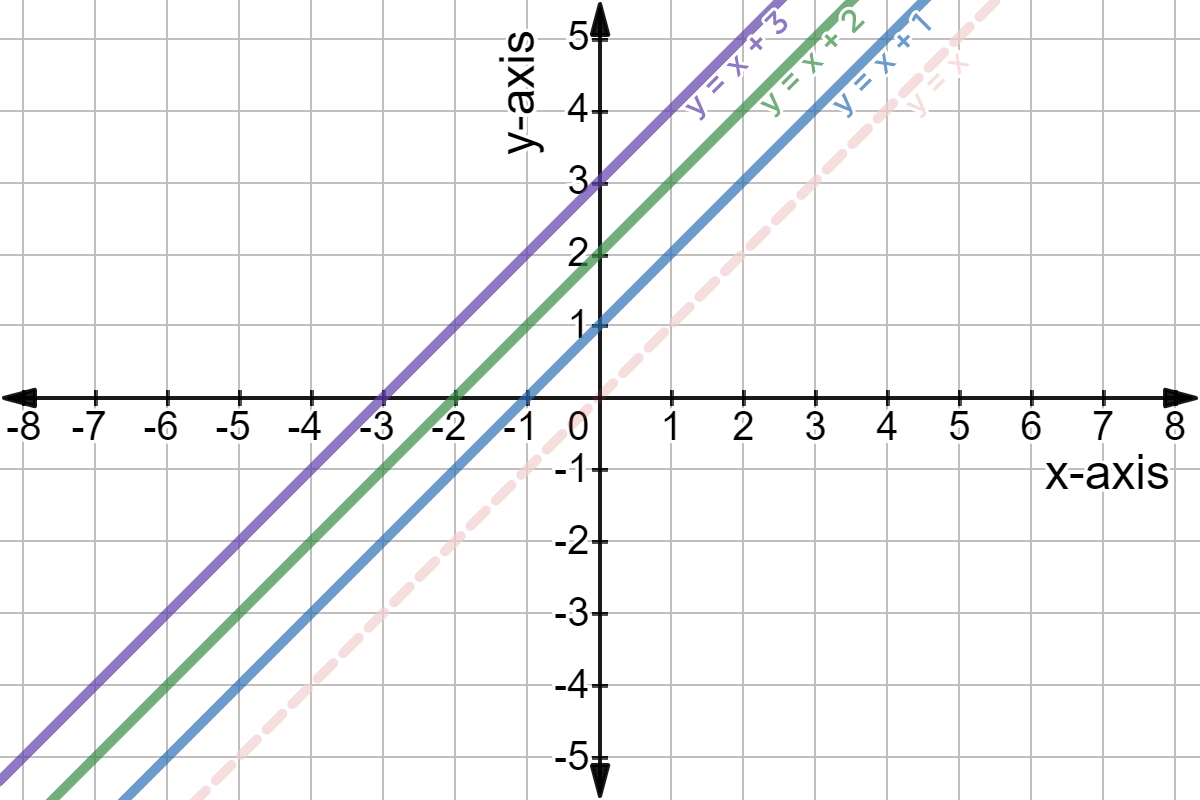



Graphing Linear Functions Expii
The graph of y ≤ x The graph of y ≥ x Examine the 3 graphs below to understand how linear inqualities relate to a linear equation Below is the graph of the equation of the line y = x 1 The equation of y ≥ x 1 The equation of y ≤ x 1 The graph of y > x 1Calculate gradients and intercepts of the graphs and then plot them to check Solve problems involving direct and inverseWe have y = 4x 3 Table of solutions X 0 1 y 3 7 We plot the points (0, 3) and (1, 7) on a graph paper and join the same by a ruler to get the line, which is the graph of the equation y = 4 x 3 This gives the work wages graph of the given equation Now, on xaxis, take a point P(4, 0) From P draw a line parallel to yaxis intersecting the work wage graph at Q



Graphing Linear Inequalities




Graph For Y X 3 Novocom Top
Which graph shows the solution to the system of linear inequalities?2 The graph of y > 3/4x 2 is a dashed line 4 One solution to the inequality is (0, 0) 5 The graph intercepts the yaxis at (0, 2)Free linear equation calculator solve linear equations stepbystep This website uses cookies to ensure you get the best experience By using this website, you agree to our Cookie Policy




Graph Of Y X 3 Novocom Top



Quadratics Graphing Parabolas Sparknotes
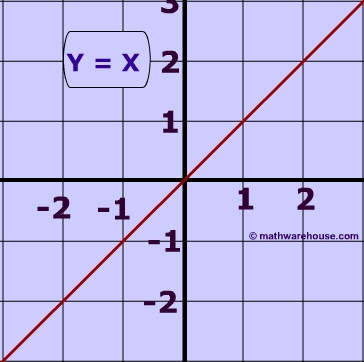
Graph the linear function f(x) = − 5 3x 6 and label the x intercept Solution From the function, we see that f(0) = 6 (or b = 6) and thus the y intercept is (0, 6) Also, we can see that the slope m = − 5 3 = − 5 3 = rise run Starting from the y intercept, mark a second point down 5 units and right 3 The inequality is y ≥ −x − 3, it means could be EQUAL OR Greater than x3 Then the line is consistent, where the 3rd graph shows that the line isThe given equation is y = – x To draw the graph of this equation, we need at least two points lying on the given line For x = 3, y = – 3, therefore, (3, – 3) satisfies the linear equation y = x For x = – 4, y = 4, therefore, ( 4, 4) satisfies the linear equation y = x
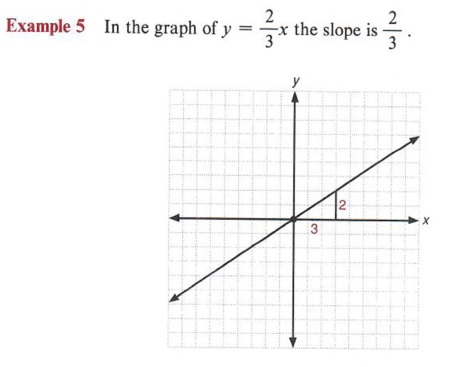



Graph Graph Inequalities With Step By Step Math Problem Solver
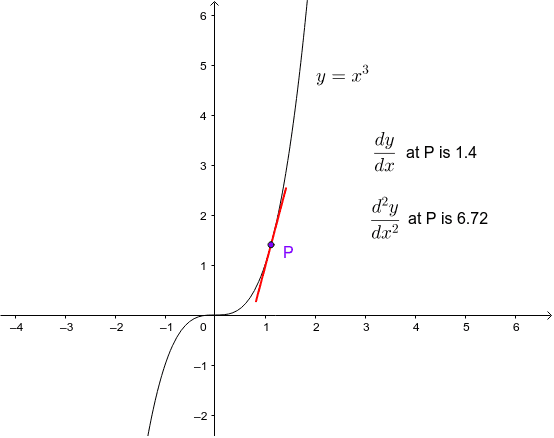



Graph Of Y X 3 Geogebra
1 We will need to rearrange this one so "y" is on its own on the left Start with 2y − x ≤ 6 Add x to both sides 2y ≤ x 6 Divide all by 2 y ≤ x/2 3 2 Now plot y = x/2 3 (as a solid line because y≤ includes equal to) Graphing Linear InequalitiesHow to Graph a Linear Inequality First, graph the "equals" line, then shade in the correct area There are three steps Rearrange the equation so "y" is on the left and everything else on the right Plot the "y=" line (make it a solid line for y≤ or y≥, and a dashed line for y< or y>) Shade above the line for a "greater than" (y> or y≥)Graphing Linear Equations Graph 4x – 3y = 12;



Solve System Of Linear Equations Graphically



Quadratic Function
There are three basic methods of graphing linear functions The first is by plotting points and then drawing a line through the points The second is by using the y intercept and slope The third is applying transformations to the identity function f (x) = x f ( x) = xAlgebra Graph y=x3 y = x 3 y = x 3 Use the slopeintercept form to find the slope and yintercept Tap for more steps The slopeintercept form is y = m x b y = m x b, where m m is the slope and b b is the yintercept y = m x b y = m x bDraw the graph of the pair of equations 2 x y = 4 and 2 x − y = 4 write the vertices of the triangle formed by these lines and the yaxis also find the area of this triangle View solution Akhila went to a fair in her village



Graphing Linear Functions Geogebra



Graphs Linear Equations Y X Example Of A Linear Function A Dog S Human S Equivalent Age A Dog S Actual Age Y X 3 21 5 35 11 77 Ppt Download
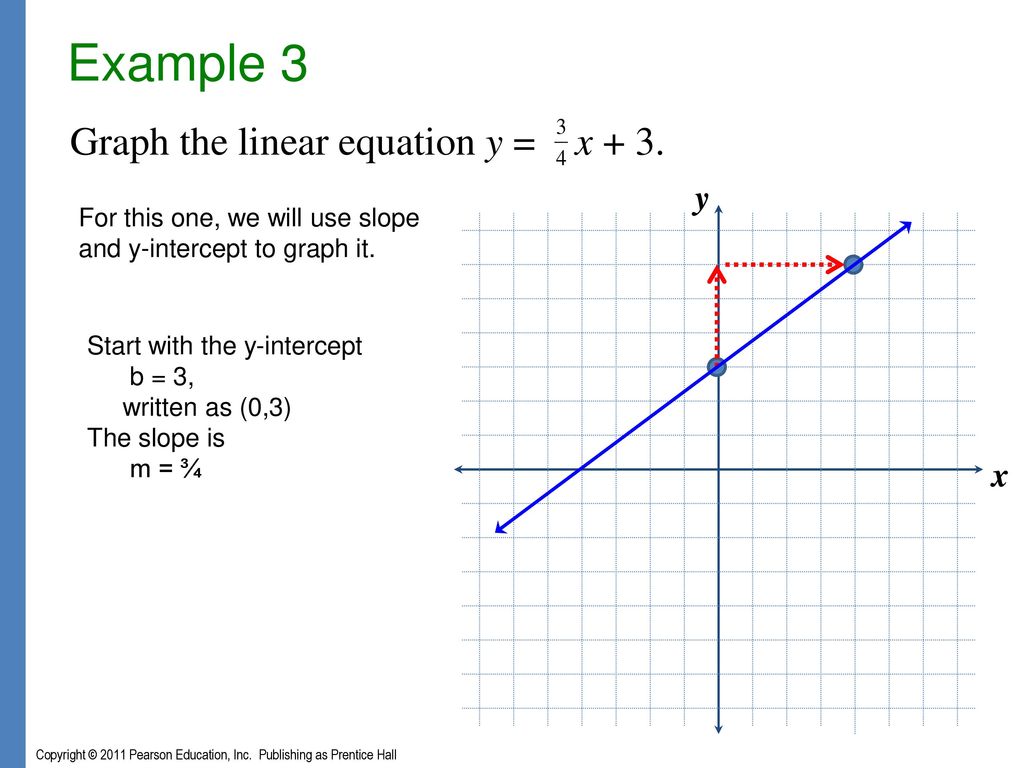
Find three points that are solutions to the equation 3 x y = − 1 First solve the equation for y y = − 3 x − 1 We'll let x x be 0, 1, and − 1 − 1 to find 3 points The ordered pairs are shown in the table below Plot the points, check that they line up, and draw the line See the figure belowGraphing a Linear Function Using yintercept and Slope Another way to graph linear functions is by using specific characteristics of the function rather than plotting points The first characteristic is its yintercept, which is the point at which the input value is zero To find the yintercept, we can set x = 0 in the equation Graphing Solutions to Linear Inequalities Solutions to linear inequalities are a shaded halfplane, bounded by a solid line or a dashed line This boundary is either included in the solution or not, depending on the given inequality {3}y
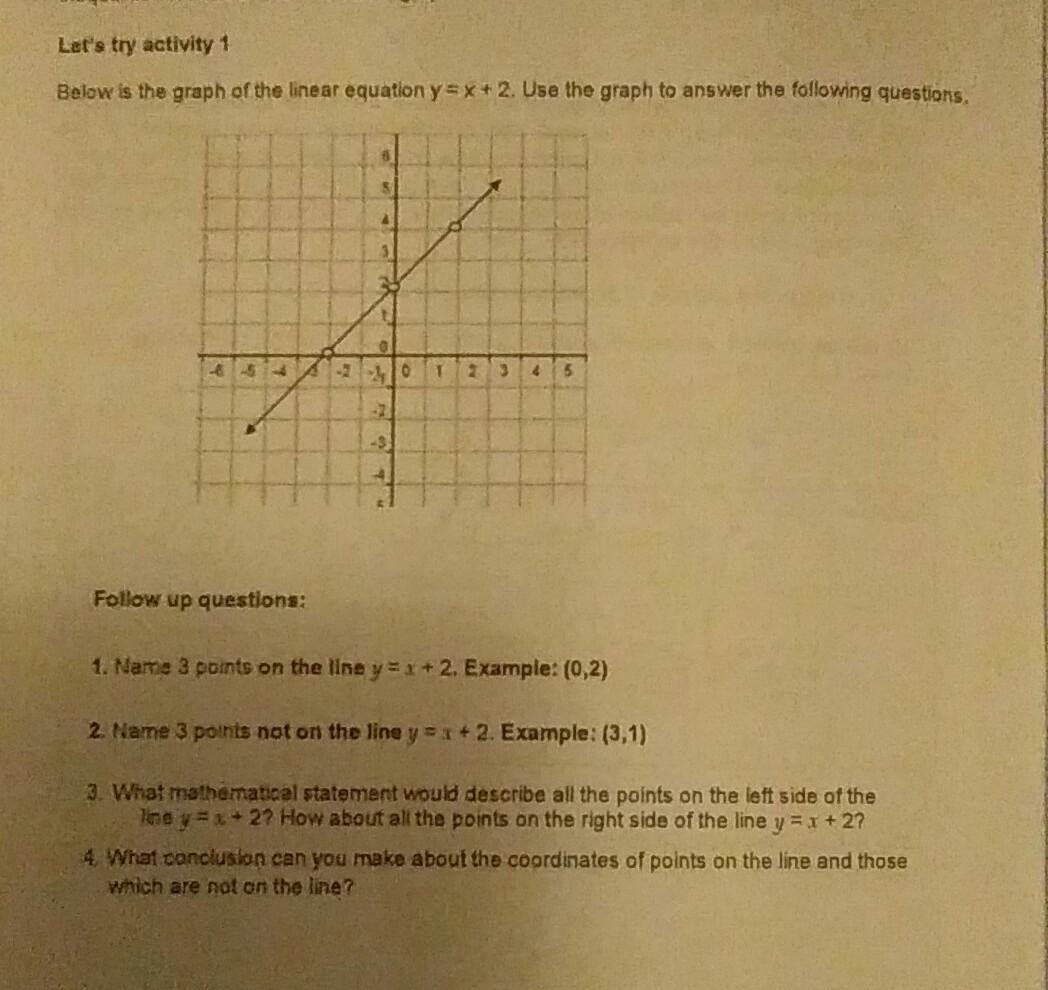



Let S Try Activity 1 Below Is The Graph Of The Linear Chegg Com



Graph Of Y X 3
The procedure to use the graphing linear equations calculator is as follows Step 1 Enter the linear equation in the input field Step 2 Now click the button "Submit" to get the graph Step 3 Finally, the graph of the given linear equation will be displayed in the new windowA linear inequality is an inequality that can be written in one of the following forms Ax By > C Ax By ≥ C Ax By < C Ax By ≤ C Where A and B are not both zero Recall that an inequality with one variable had many solutions For example, the solution to the inequality x > 3 is any number greater than 3 LINEAR EQUATION An equation of the form A x B y = C, where A and B are not both zero, is called a linear equation in two variables Here is an example of a linear equation in two variables, x and y The equation y = − 3 x 5 is also a linear equation But it does not appear to be in the form A x B y = C




Graph Graph Inequalities With Step By Step Math Problem Solver



Linear Inequalities How To Graph The Equation Of A Linear Inequality
Section 31 Graphing Systems of Linear Inequalities in Two Variables Procedure for Graphing Linear Inequalities 1 Draw the graph of the equation obtained for the given inequality by replacing the inequality sign with an equal sign Use a dashed line if the problem involves a



Quadratics Graphing Parabolas Sparknotes




Graph Y 3 5 X 2 Youtube




Quadratic Function



1 3 Coordinate Plane And Graphing Equations Hunter College Math101



Draw The Graph Of The Equation 2x Y 3 0 Using The Graph Find T




Graphing Linear Inequalities




Draw Graph Of The Equation Y X 5




Which System Of Linear Inequalities Is Represented By The Graph Y Gt X 3 And 3x Y Gt 2 Y Brainly Com




Which System Of Linear Inequalities Is Represented By The Graph Y Gt One Thirdx 3 And 3x Y Brainly Com




Draw The Graph Of The Equation X Y 3 And Y X 1 What Do You



How Do You Solve Each Linear System By Graphing Y X 3 Y 2x 6 Mathskey Com



Solution Graph The Equation And Identify The Y Intercept Y X 3 Thank You For Your Time




5 2 Reference Graphs Of Eight Basic Types Of Functions



How Do You Graph The Function Y X 3 Socratic



Linear Inequalities How To Graph The Equation Of A Linear Inequality



3 Graphical Solution Of A System Of Linear Equations



Solution Solve The Linear System By Graphing Check You Solution Y X 1 Y 3x 9




Graph Y X 2 3 Youtube



Graph Graph Equations With Step By Step Math Problem Solver



Draw The Graphs Of Linear Equations Y X And Y X On The Same Cartesian Plane Studyrankersonline




Which Graph Shows The Solution To The System Of Linear Inequalities Y Gt 2 3x 3 Y 1 3x 2 Brainly Com



Solution Are These Equations Linear And If Not Explain X 2 Y 7 G X 2 X 3 X 3 Y F X 7




Draw The Graph Of Y X 3 Novocom Top




Graph Linear Equations In Two Variables Intermediate Algebra



Graphing Linear Equations Ppt Video Online Download



Chapter 3 Graphs And Functions Ppt Download
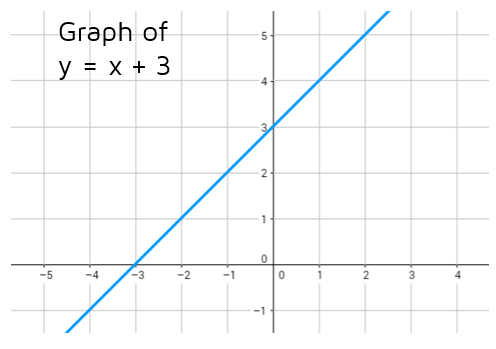



Graphing Linear Inequalities Kate S Math Lessons
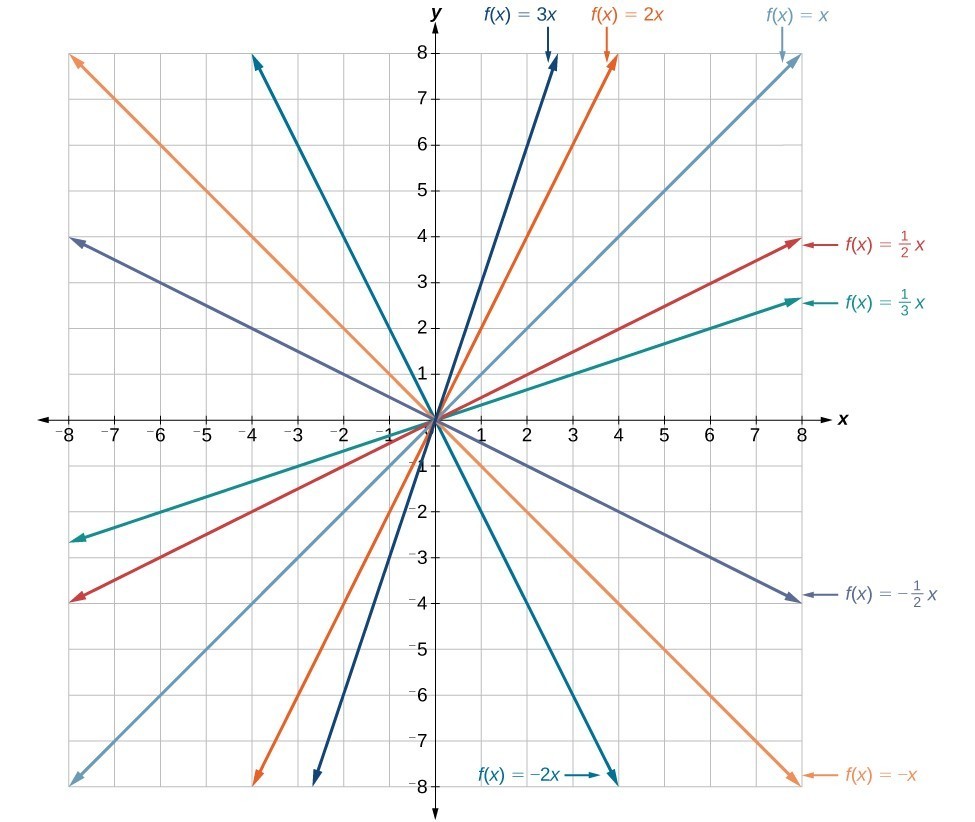



Read Transform Linear Functions Intermediate Algebra
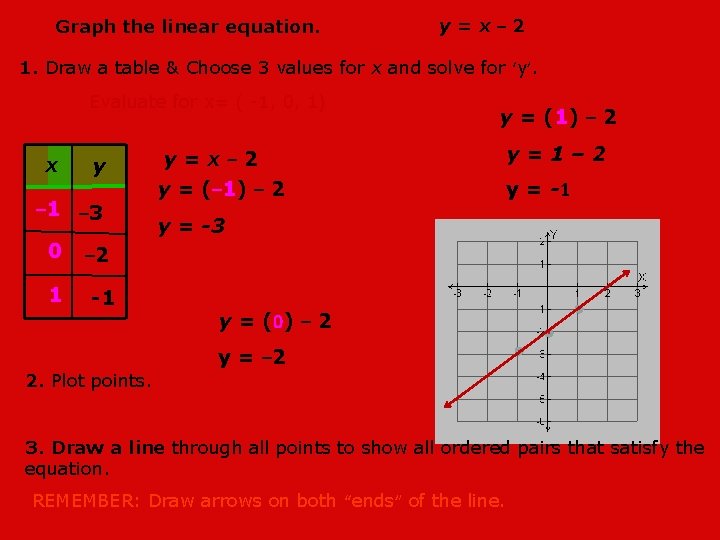



Graph The Linear Equation Yx 2 1 Draw
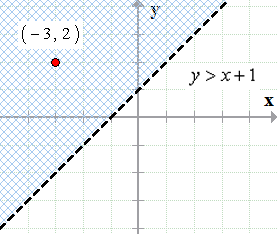



Graphing Linear Inequalities Chilimath
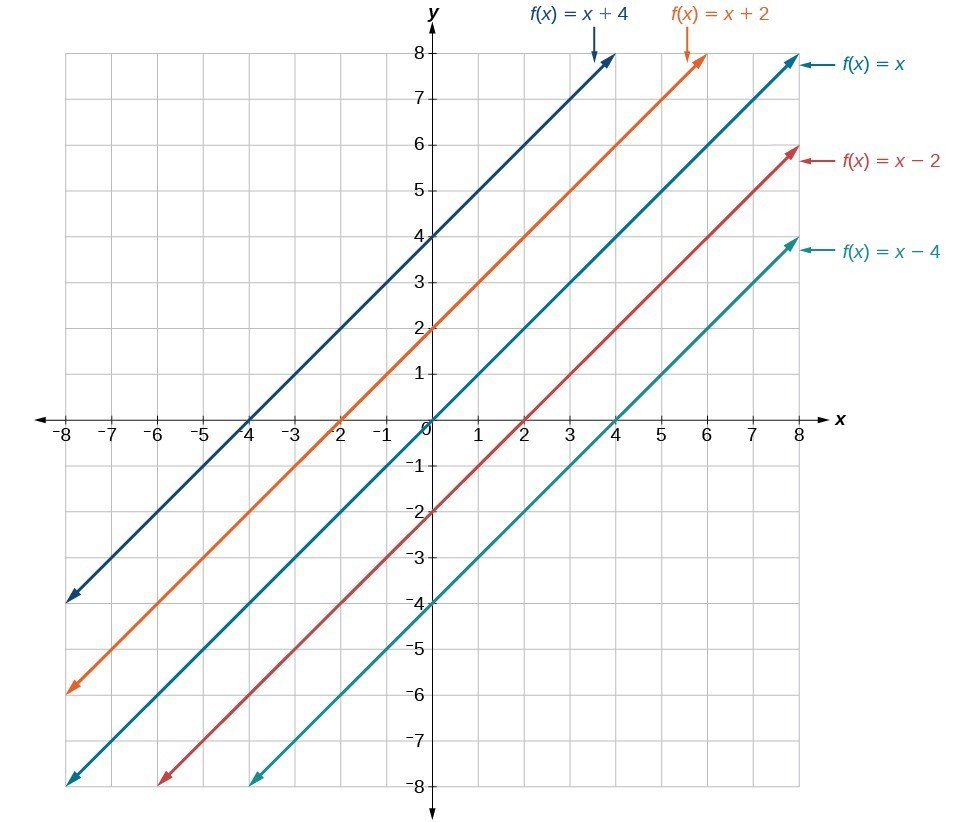



Read Transform Linear Functions Intermediate Algebra
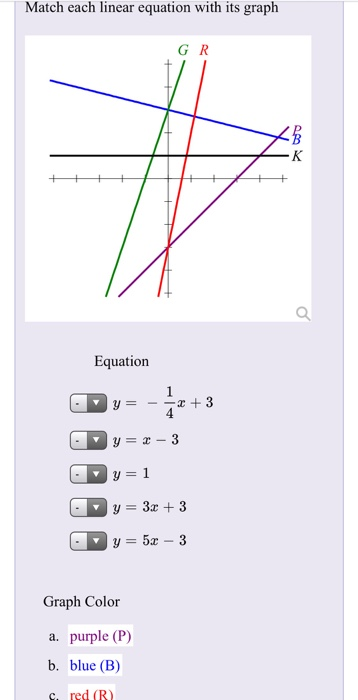



Match Each Linear Equation With Its Graph Gr Haha Chegg Com
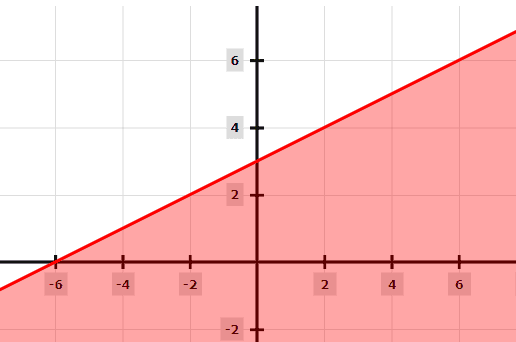



Graphing Linear Inequalities Explanation Examples
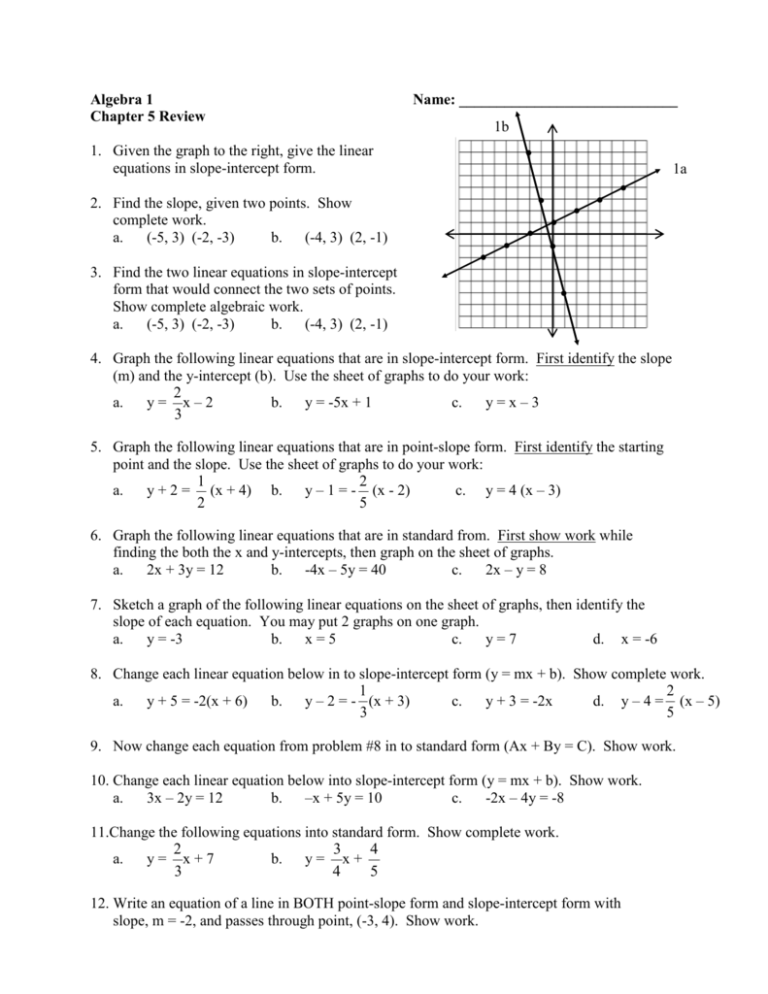



Algebra 1 Name 1a 1b Chapter 5 Review Given The Graph To The
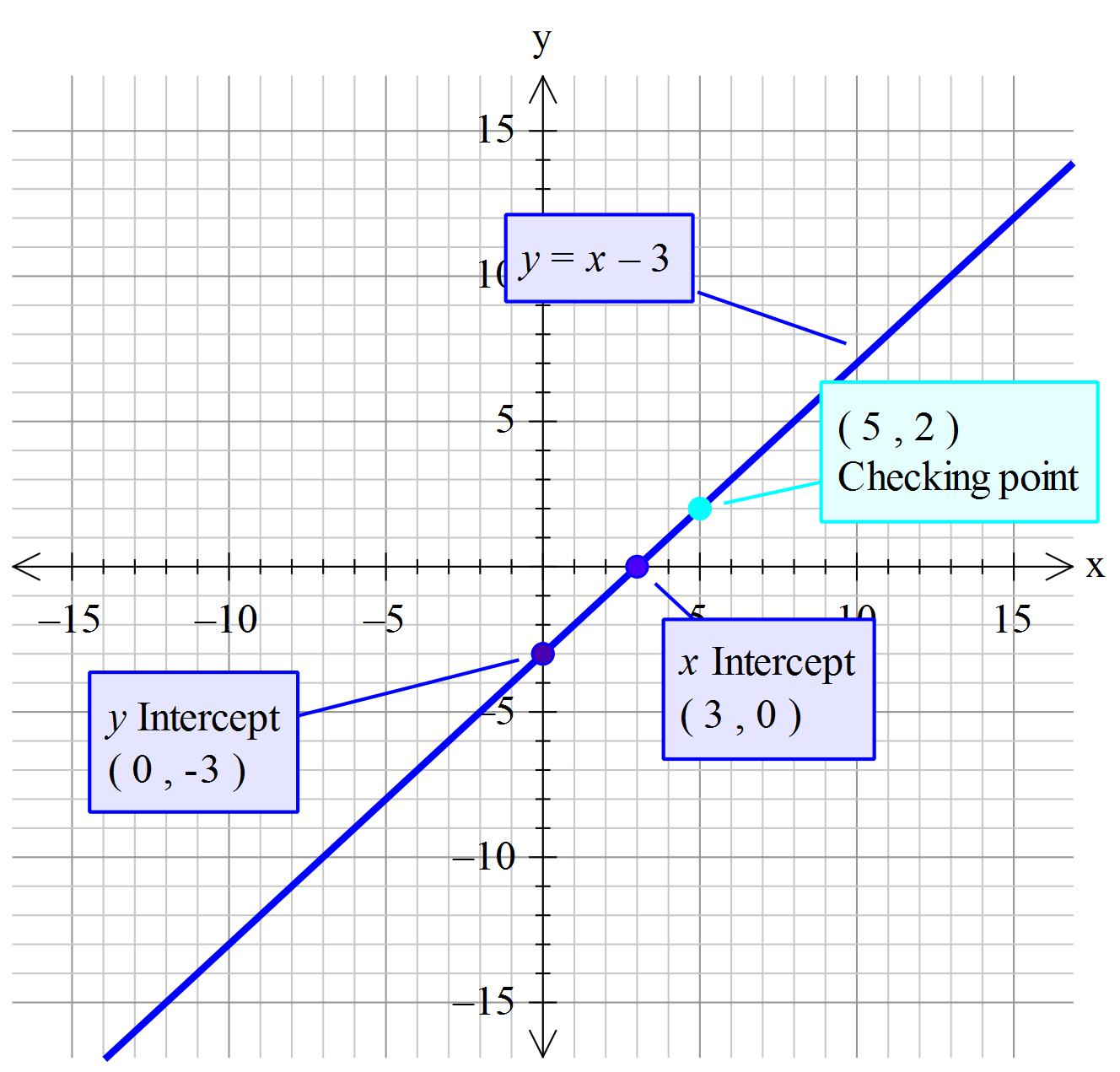



How Do You Graph Y X 3 Example



Graphfory Fontface Symbol Font X 3




The Graph Of Y X 3 Is Shown Below The Figure Shows Chegg Com
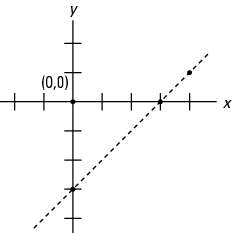



Linear Inequalities And Half Planes
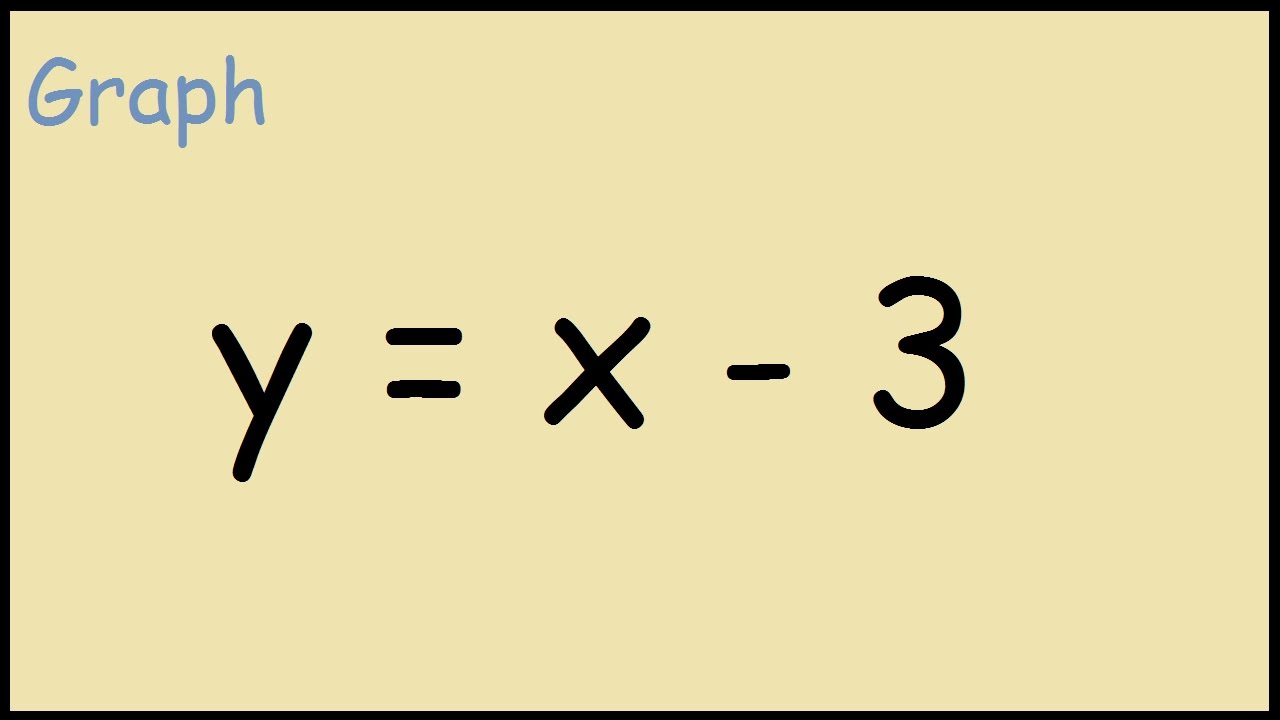



How To Graph Y X 3 Youtube
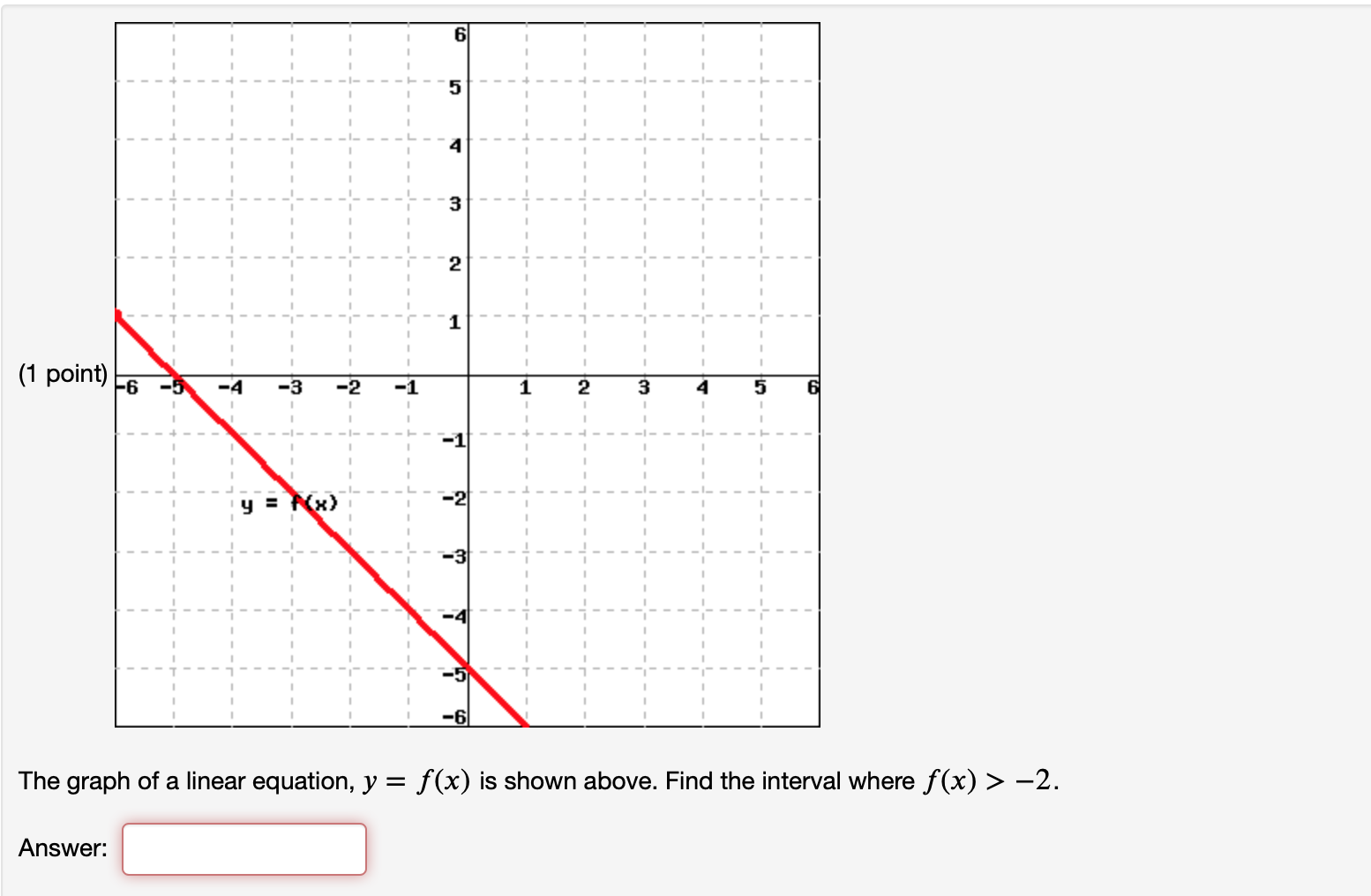



Solved 6 5 3 2 1 Point 6 4 3 2 1 2 3 4 5 Y X 3 Chegg Com
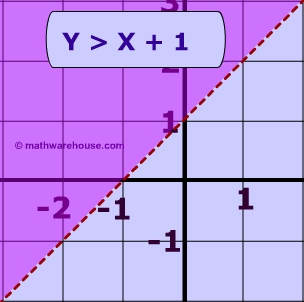



Linear Inequalities How To Graph The Equation Of A Linear Inequality



Graph Graph Equations With Step By Step Math Problem Solver
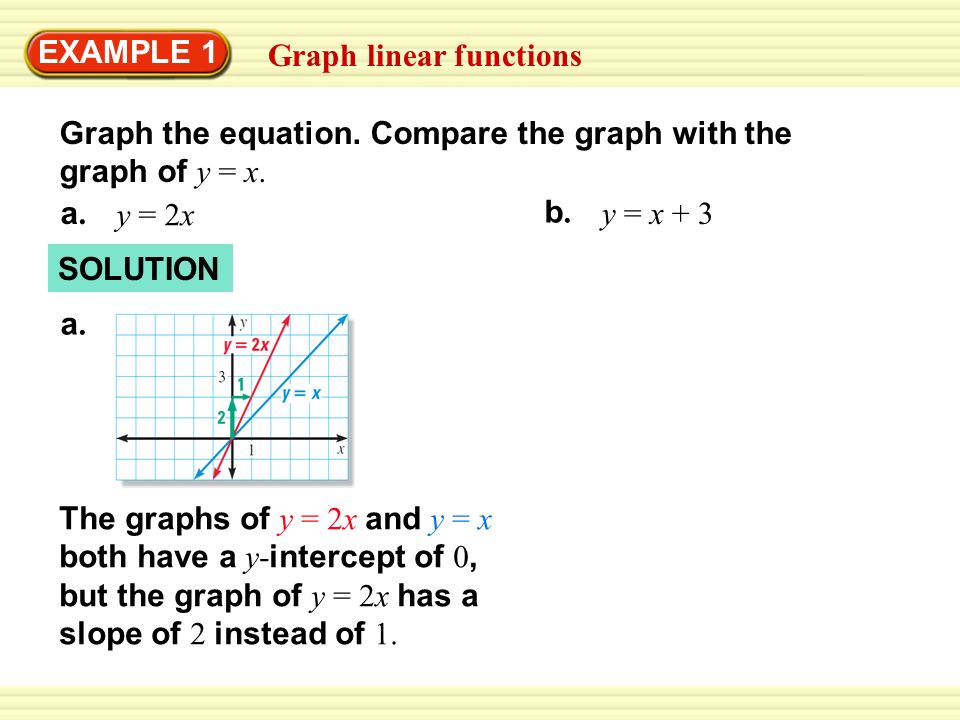



Chapter 2 Section 3 Graph Linear Functions Example 1 Graph The Equation Compare The Graph With The Graph Of Y X A A Y 2x B B Y X 3 Solution Ppt Download
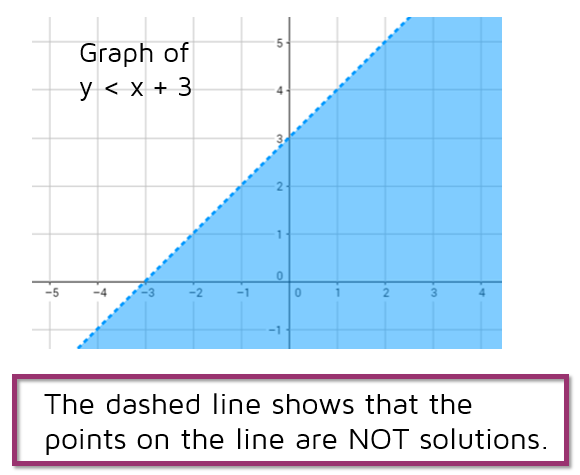



Graphing Linear Inequalities Kate S Math Lessons
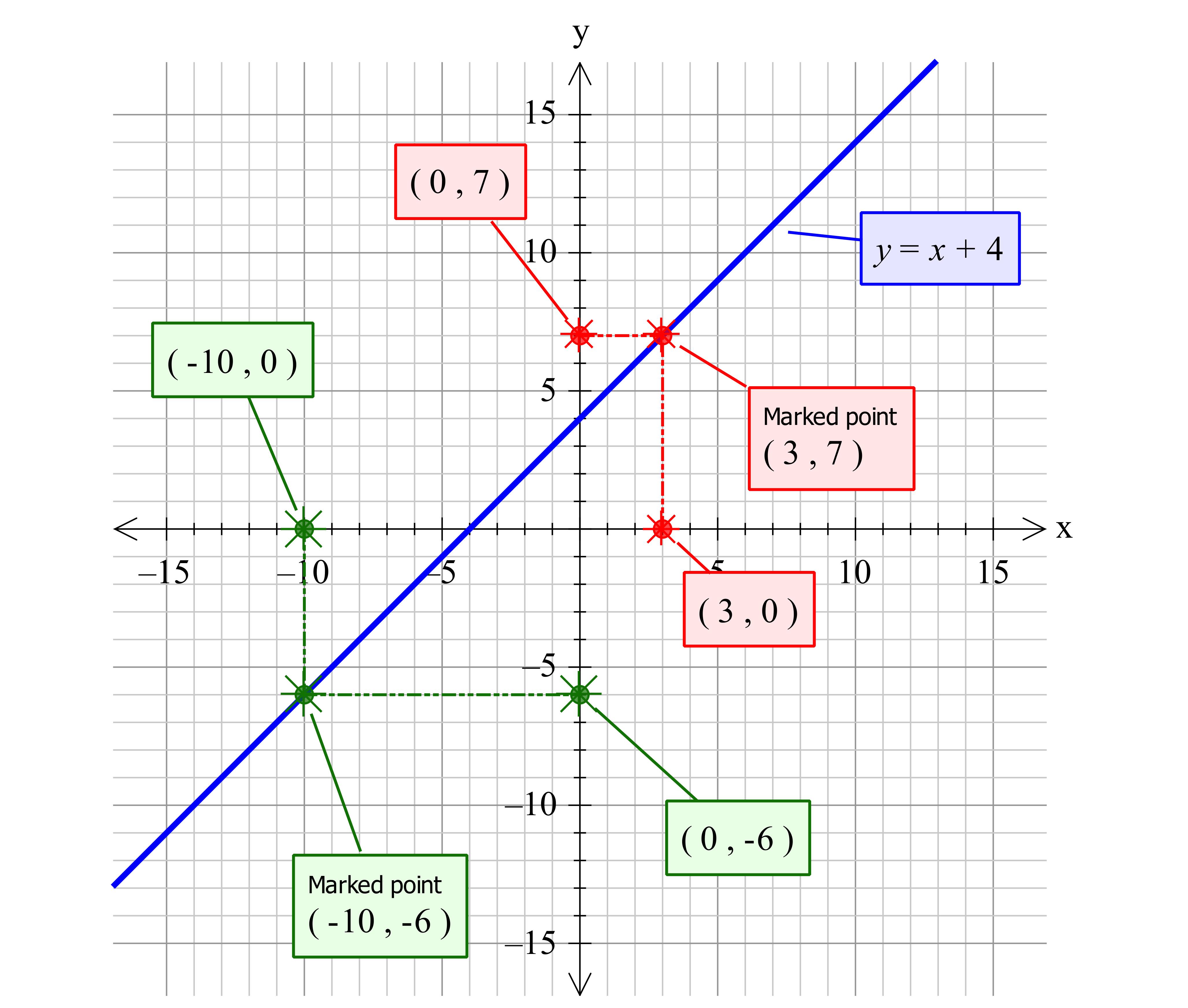



How Do You Graph Y X 4 Socratic




Graphing Linear Inequalities




Linear Inequalities Alg 1 P 6 Ochs 14 15



How Do You Graph The Inequality Y 3 Socratic




Below Is The Graph Of Y X 3 Translate It To Make Chegg Com
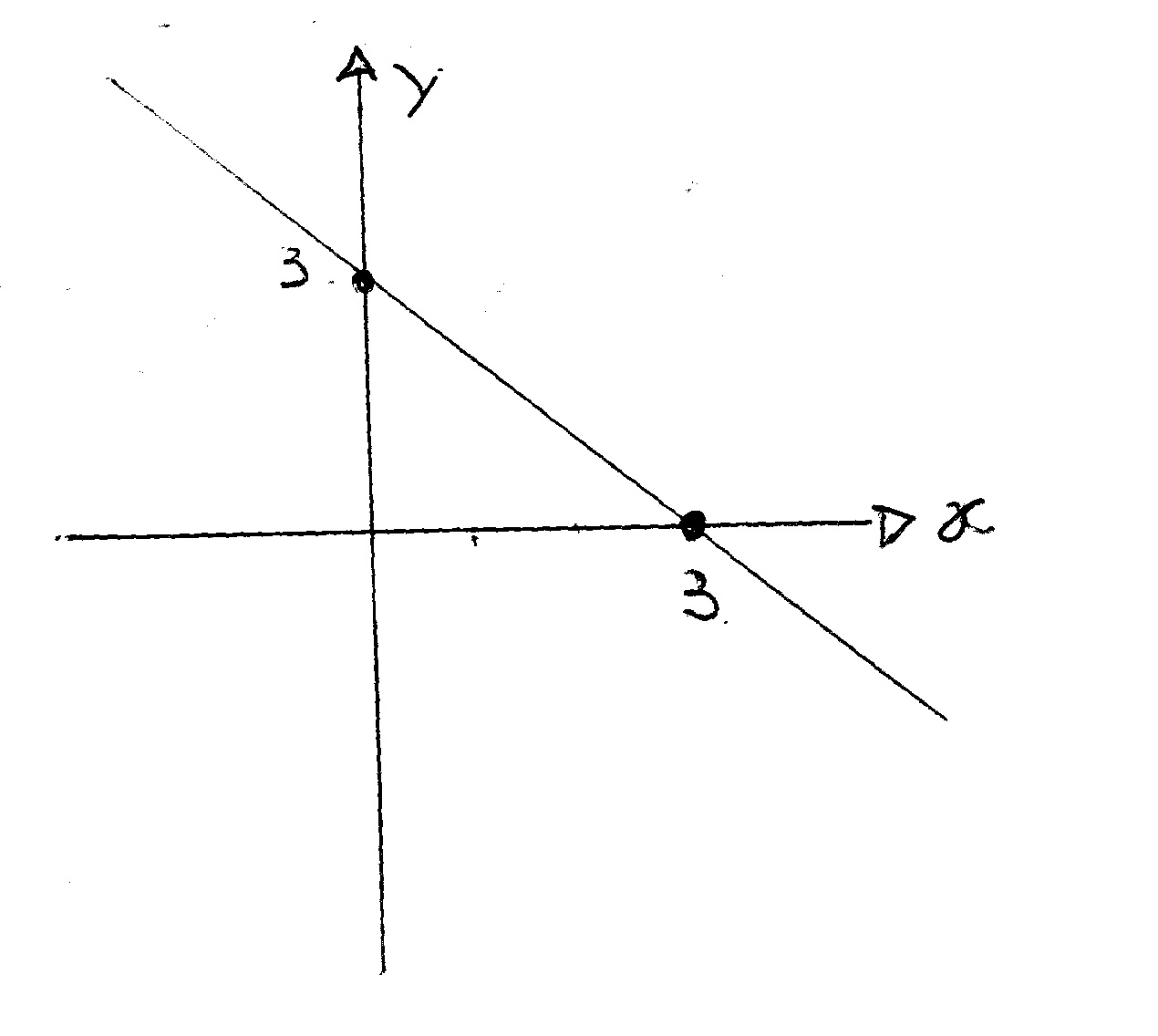



How Do You Graph The Equation Y X 3 Socratic




Systems Of Equations With Graphing Article Khan Academy
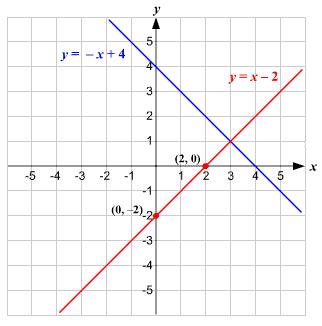



Solve System Of Linear Equations Graphically
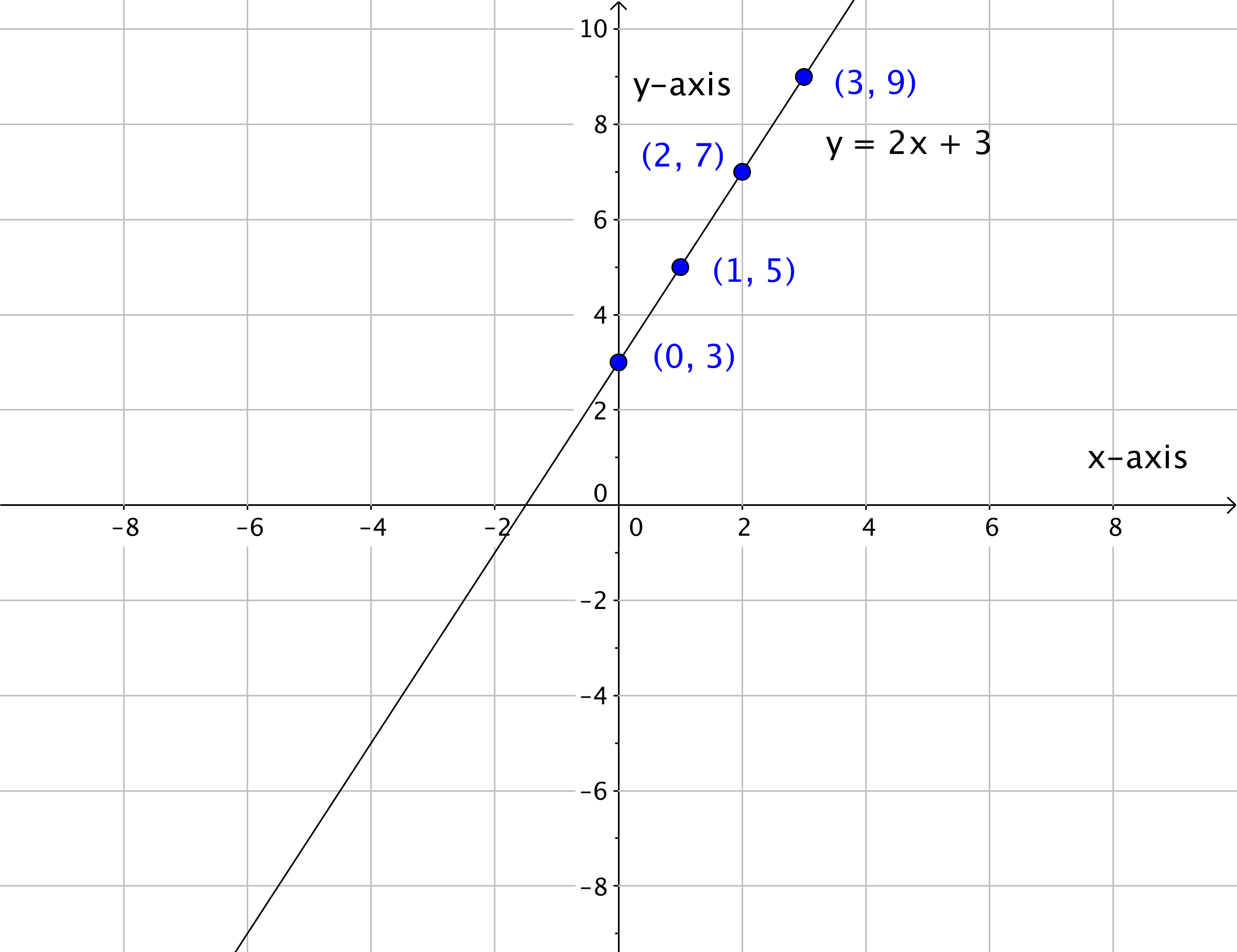



1 3 Coordinate Plane And Graphing Equations Hunter College Math101




Y X 3 4 Graph Novocom Top
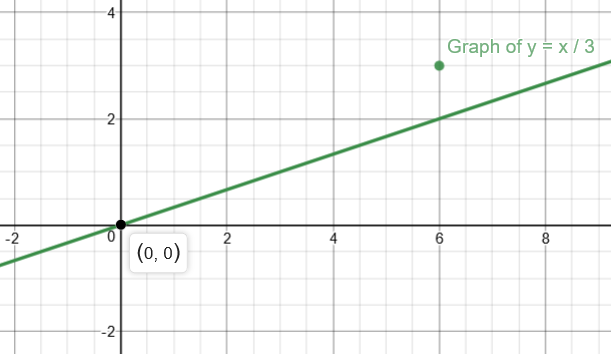



How Do You Graph Y X 3 1 Socratic




Graphs Of Linear Functions Precalculus I




Graphing Linear And Nonlinear Equations With Tables Of Values Worksheet Equations Values Worksheet Graphing




How To Graph The Line Y X Youtube
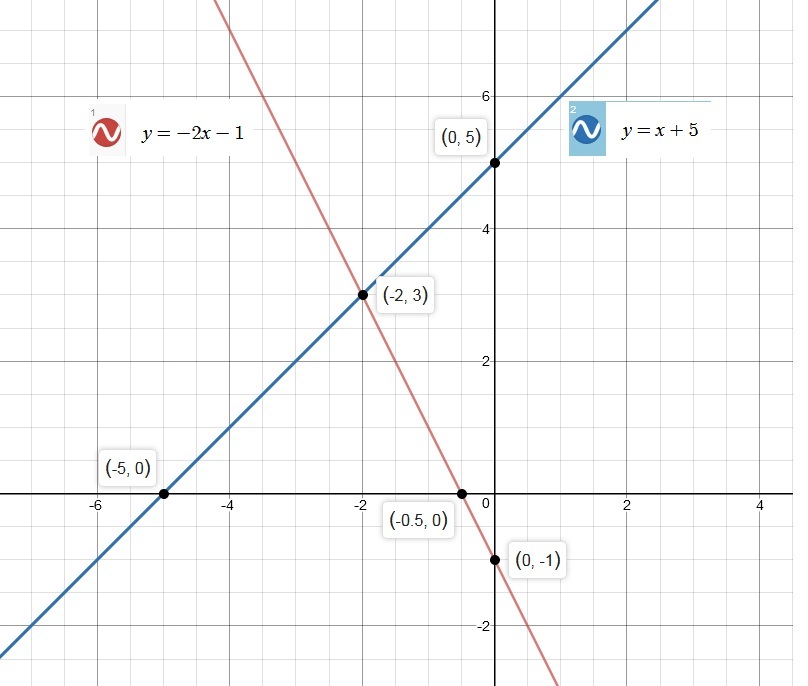



How Do You Solve The System By Graphing Y 2x 1 And Y X 5 Socratic




Which Is The Graph Of The Linear Inequality Y X 3 Brainly Com
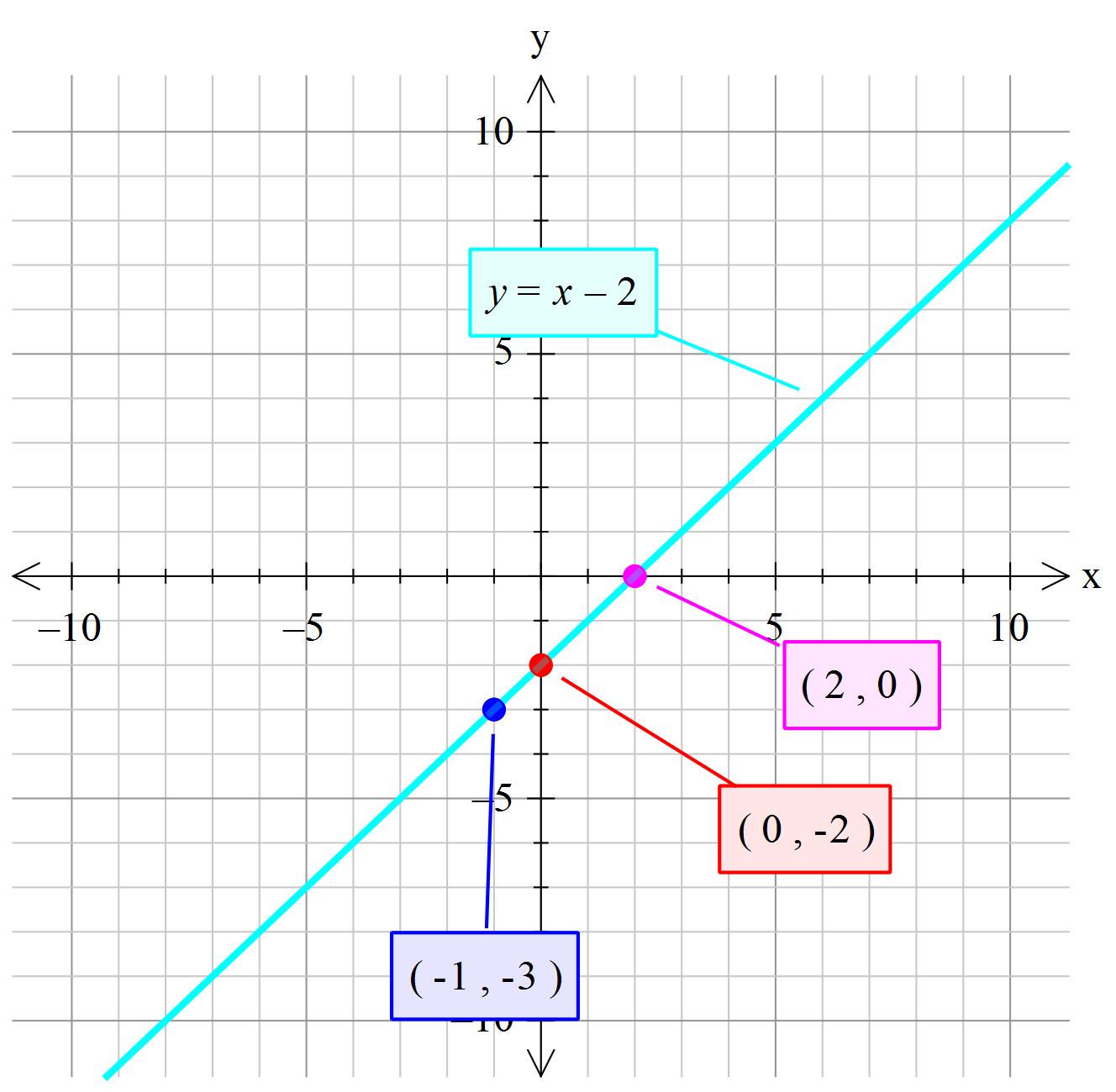



How Do You Graph The Line X Y 2 Socratic
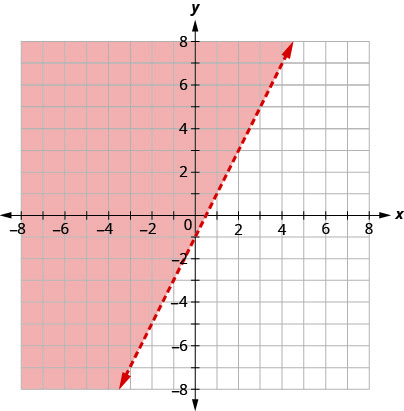



4 1 Graphing Linear Inequalities In Two Variables Mathematics Libretexts



Solution 3 Graph I Am So Confused I Can Get The Problem But I Can 39 T Draw Up The Graph P 0 3 Is The Intersection Where The Lines Cross 1st Line




Draw The Graph Of Each Of The Following Linear Equations And Answer The Following Question I Y X Ii Y 2x Iii Y 2x Iv Y 3x V
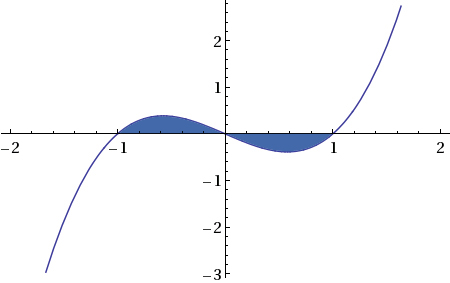



The Area Bounded By The Curve Y X 3 X And The X Axis Emathzone
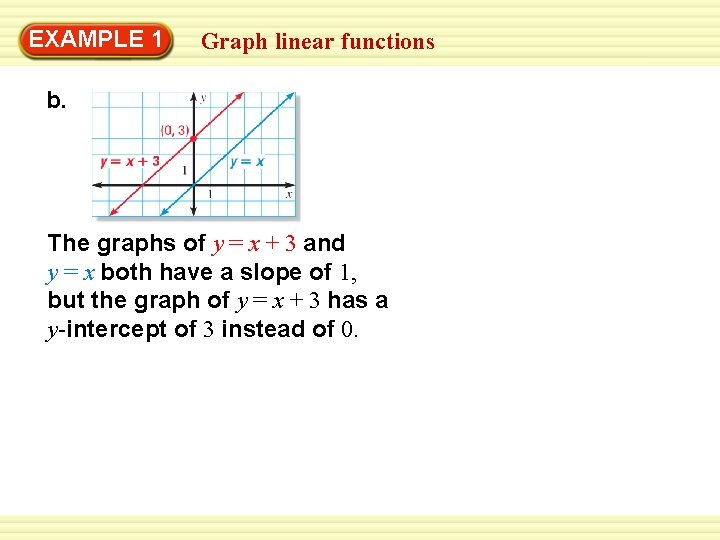



Example 1 Graph Linear Functions Graph The Equation
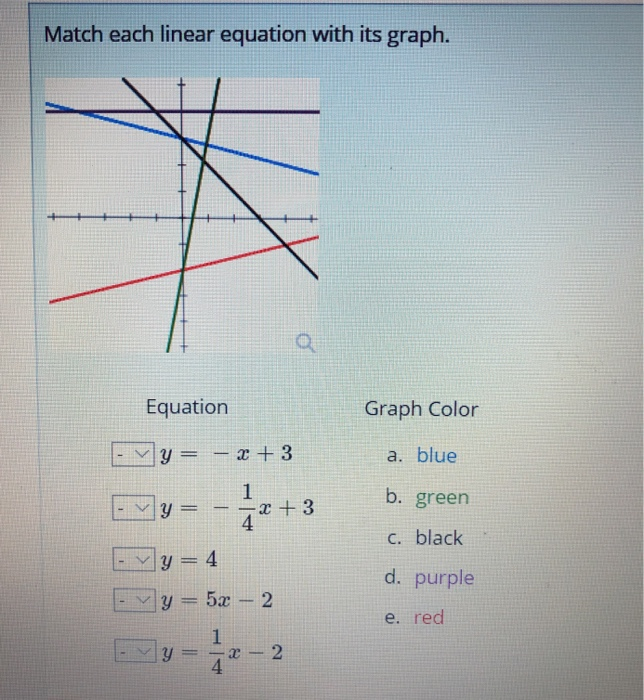



Solved Match Each Linear Equation With Its Graph Equatio Chegg Com



Graphing Quadratic Functions




Which Of The Following Is The Graph Of The Equation Y X 3 Pakisgot Po Brainly Ph




Which Graph Represents The Linear Function Y X 3 4 4 Brainly Com
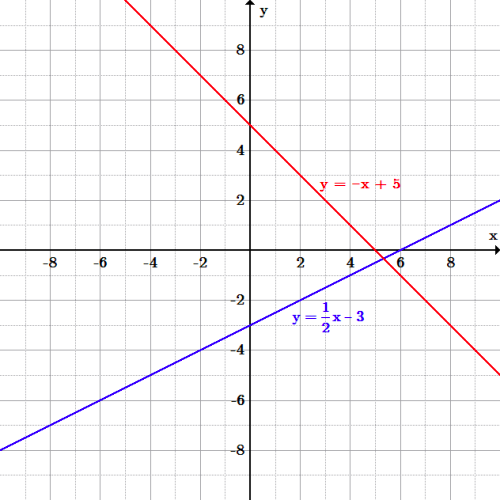



Introduction To Linear Functions Boundless Algebra


